
【题目】已知曲线![]() ,直线
,直线![]() (其中
(其中![]() )与曲线
)与曲线![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(Ⅰ)若![]() ,试判断曲线
,试判断曲线![]() 的形状.
的形状.
(Ⅱ)若![]() ,以线段
,以线段![]() 、
、![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,其中顶点
,其中顶点![]() 在曲线
在曲线![]() 上,
上, ![]() 为坐标原点,求
为坐标原点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)答案见解析;(Ⅱ) ![]() .
.
【解析】试题分析:
(Ⅰ)结合所给的方程讨论可得:
当![]() 时,曲线
时,曲线![]() 的形状为直线
的形状为直线![]() ,
,
当![]() 时,曲线表示以焦点在
时,曲线表示以焦点在![]() 轴上,以
轴上,以![]() 为实轴,以
为实轴,以![]() 为焦距的双曲线,
为焦距的双曲线,
当![]() 时,表示焦点在
时,表示焦点在![]() 轴上,以
轴上,以![]() 为长轴,以
为长轴,以![]() 为焦距的椭圆,
为焦距的椭圆,
当![]() 时,表示焦点在
时,表示焦点在![]() 轴上,以
轴上,以![]() 为长轴,以
为长轴,以![]() 为焦距的椭圆,
为焦距的椭圆,
当![]() 时,表示圆心在原点,以
时,表示圆心在原点,以![]() 为半径的圆.
为半径的圆.
(Ⅱ)当![]() 时,曲线方程为:
时,曲线方程为: ![]() ,分类讨论:
,分类讨论:
当![]() 时,
时, ![]() ,
,
当![]() 时,联立直线与椭圆的方程,消去
时,联立直线与椭圆的方程,消去![]() 整理变形,结合题意可得
整理变形,结合题意可得![]() ,结合
,结合![]() ,可得
,可得![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(Ⅰ)当![]() 时,
时, ![]() ,
, ![]() ,曲线
,曲线![]() 的形状为直线
的形状为直线![]() ,
,
当![]() 时,
时, ![]() ,表示以焦点在
,表示以焦点在![]() 轴上,以
轴上,以![]() 为实轴,
为实轴,
以![]() 为焦距的双曲线,
为焦距的双曲线,
当![]() 时,
时, ![]() ,
,
当![]() ,即
,即![]() 时,表示焦点在
时,表示焦点在![]() 轴上,以
轴上,以![]() 为长轴,以
为长轴,以![]() 为焦距的椭圆,
为焦距的椭圆,
当![]() ,即
,即![]() 时,表示焦点在
时,表示焦点在![]() 轴上,以
轴上,以![]() 为长轴,以
为长轴,以![]() 为焦距的椭圆,
为焦距的椭圆,
当![]() ,即
,即![]() 时,表示圆心在原点,以
时,表示圆心在原点,以![]() 为半径的圆.
为半径的圆.
(Ⅱ)当![]() 时,曲线方程为:
时,曲线方程为: ![]() ,
,
当![]() 时,
时, ![]() 在椭圆
在椭圆![]() 上,计算得出
上,计算得出![]() ,
,
∴![]() ,
,
当![]() 时,则
时,则 ,消去
,消去![]() 化简整理得:
化简整理得:
![]() ,
,
![]() ①,
①,
设![]() ,
, ![]() ,
, ![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,
,
因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,
,
从而 ,化简得:
,化简得: ![]() ,
,
经检验满足①式,
又![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上, ![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50],[50,60],…,[80,90],[90,100] 
(1)求频率分布图中a的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在[40,60]的受访职工中,随机抽取2人,求此2人评分都在[40,50]的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(cosx,﹣
=(cosx,﹣ ![]() ),
), ![]() =(sinx+cosx,1),f(x)=
=(sinx+cosx,1),f(x)= ![]()
![]() ,
,
(1)若0<α< ![]() ,sinα=
,sinα= ![]() ,求f(α)的值;
,求f(α)的值;
(2)求函数f(x)的最小正周期及单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π),在同一周期内,当x= ![]() 时,f(x)取得最大值3;当x=
时,f(x)取得最大值3;当x= ![]() 时,f(x)取得最小值﹣3.
时,f(x)取得最小值﹣3.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是等差数列,{bn}是各项都为正数的等比数列,且a1=b1=1,a3+b5=21,a5+b3=13.
(1)求{an}、{bn}的通项公式;
(2)求数列 ![]() 的前n项和Sn .
的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中, ![]() ,
, ![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻转成
翻转成![]() .若
.若![]() 为线段
为线段![]() 的中点,则在
的中点,则在![]() 翻折过程中:
翻折过程中:
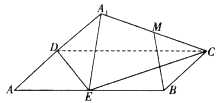
①![]() 是定值;②点
是定值;②点![]() 在某个球面上运动;
在某个球面上运动;
③存在某个位置,使![]() ;④存在某个位置,使
;④存在某个位置,使![]() 平面
平面![]() .
.
其中正确的命题是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com