
ЎҫМвДҝЎҝ№уСфУлҝӯАпБҪөШПаҫаФј200З§ГЧЈ¬Т»Бҫ»хіөҙУ№уСфФИЛЩРРК»өҪҝӯАпЈ¬№ж¶ЁЛЩ¶ИІ»өГі¬№э100З§ГЧ![]() КұЈ¬ТСЦӘ»хіөГҝРЎКұөДФЛКдіЙұҫ
КұЈ¬ТСЦӘ»хіөГҝРЎКұөДФЛКдіЙұҫ![]() ТФФӘОӘөҘО»
ТФФӘОӘөҘО»![]() УЙҝЙұдІҝ·ЦәН№М¶ЁІҝ·ЦЧйіЙЈәҝЙұдІҝ·ЦУлЛЩ¶И
УЙҝЙұдІҝ·ЦәН№М¶ЁІҝ·ЦЧйіЙЈәҝЙұдІҝ·ЦУлЛЩ¶И![]() З§ГЧ
З§ГЧ![]() Кұ
Кұ![]() өДЖҪ·ҪіЙХэұИЈ¬ұИАэПөКэОӘ
өДЖҪ·ҪіЙХэұИЈ¬ұИАэПөКэОӘ![]() Ј»№М¶ЁІҝ·ЦОӘ64ФӘЈ®
Ј»№М¶ЁІҝ·ЦОӘ64ФӘЈ®
![]() °СИ«іМФЛКдіЙұҫ
°СИ«іМФЛКдіЙұҫ![]() ФӘ
ФӘ![]() ұнКҫОӘЛЩ¶И
ұнКҫОӘЛЩ¶И![]() З§ГЧ
З§ГЧ![]() Кұ
Кұ![]() өДәҜКэЈ¬ІўЦёіцХвёцәҜКэөД¶ЁТеУтЈ»
өДәҜКэЈ¬ІўЦёіцХвёцәҜКэөД¶ЁТеУтЈ»
![]() ОӘБЛК№И«іМФЛКдіЙұҫЧоРЎЈ¬»хіөУҰТФ¶аҙуЛЩ¶ИРРК»Јҝ
ОӘБЛК№И«іМФЛКдіЙұҫЧоРЎЈ¬»хіөУҰТФ¶аҙуЛЩ¶ИРРК»Јҝ
Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј»ЈЁ2Ј©
Ј»ЈЁ2Ј©![]() .
.
ЎҫҪвОцЎҝ
![]() Зуіц»хіөҙУ№уСфФИЛЩРРК»өҪҝӯАпЛщУГКұјдЈ¬ёщҫЭ»хіөГҝРЎКұөДФЛКдіЙұҫ
Зуіц»хіөҙУ№уСфФИЛЩРРК»өҪҝӯАпЛщУГКұјдЈ¬ёщҫЭ»хіөГҝРЎКұөДФЛКдіЙұҫ![]() ТФФӘОӘөҘО»
ТФФӘОӘөҘО»![]() УЙҝЙұдІҝ·ЦәН№М¶ЁІҝ·ЦЧйіЙЈ¬ҝЙөГИ«іМФЛКдіЙұҫЈ¬ј°әҜКэөД¶ЁТеУтЈ»
УЙҝЙұдІҝ·ЦәН№М¶ЁІҝ·ЦЧйіЙЈ¬ҝЙөГИ«іМФЛКдіЙұҫЈ¬ј°әҜКэөД¶ЁТеУтЈ»
![]() АыУГ»щұҫІ»өИКҪ
АыУГ»щұҫІ»өИКҪ![]() Ј¬
Ј¬![]() КұИЎөГөИәЕ
КұИЎөГөИәЕ![]() Ј¬ҝЙөГ
Ј¬ҝЙөГ![]() З§ГЧ
З§ГЧ![]() КұЈ¬И«іМФЛКдіЙұҫЧоРЎЈ®
КұЈ¬И«іМФЛКдіЙұҫЧоРЎЈ®
![]() ТАМвТвТ»Бҫ»хіөҙУ№уСфФИЛЩРРК»өҪҝӯАпЛщУГКұјдОӘ
ТАМвТвТ»Бҫ»хіөҙУ№уСфФИЛЩРРК»өҪҝӯАпЛщУГКұјдОӘ![]() Ј¬
Ј¬
И«іМФЛКдіЙұҫОӘ![]() Ј¬
Ј¬
ЛщЗуәҜКэ¶ЁТеУтОӘ![]() Ј»
Ј»
![]() ТАМвТвЦӘ
ТАМвТвЦӘ![]() Ј¬
Ј¬
№КУР![]() Ј¬
Ј¬
өұЗТҪцөұ![]() Ј¬јҙ
Ј¬јҙ![]() КұЈ¬өИәЕіЙБўЈ®
КұЈ¬өИәЕіЙБўЈ®
№Көұ![]() З§ГЧ
З§ГЧ![]() КұЈ¬И«іМФЛКдіЙұҫЧоРЎЈ®
КұЈ¬И«іМФЛКдіЙұҫЧоРЎЈ®


 ФД¶БҝміөПөБРҙр°ё
ФД¶БҝміөПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝјЗәҜКэf(x)ЈҪ![]() өД¶ЁТеУтОӘјҜәПAЈ¬әҜКэg(x)ЈҪ
өД¶ЁТеУтОӘјҜәПAЈ¬әҜКэg(x)ЈҪ![]() ФЪ(0Ј¬Ј«ЎЮ)ЙПОӘФцәҜКэКұkөДИЎЦөјҜәПОӘBЈ¬әҜКэh(x)ЈҪx2Ј«2xЈ«4өДЦөУтОӘјҜәПC.
ФЪ(0Ј¬Ј«ЎЮ)ЙПОӘФцәҜКэКұkөДИЎЦөјҜәПОӘBЈ¬әҜКэh(x)ЈҪx2Ј«2xЈ«4өДЦөУтОӘјҜәПC.
(1)ЗујҜәПAЈ¬BЈ¬CЈ»
(2)ЗујҜәПAЎИ(RB)Ј¬AЎЙ(BЎИC)Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘНЦФІ![]() ЙПөДөгөҪЛьөДБҪёцҪ№өДҫаАлЦ®әНОӘ
ЙПөДөгөҪЛьөДБҪёцҪ№өДҫаАлЦ®әНОӘ![]() Ј¬ТФНЦФІ
Ј¬ТФНЦФІ![]() өД¶МЦбОӘЦұҫ¶өДФІ
өД¶МЦбОӘЦұҫ¶өДФІ![]() ҫӯ№эХвБҪёцҪ№өгЈ¬өг
ҫӯ№эХвБҪёцҪ№өгЈ¬өг![]() Ј¬
Ј¬ ![]() ·ЦұрКЗНЦФІ
·ЦұрКЗНЦФІ![]() өДЧуЎўУТ¶ҘөгЈ®
өДЧуЎўУТ¶ҘөгЈ®
ЈЁ![]() Ј©ЗуФІ
Ј©ЗуФІ![]() әННЦФІ
әННЦФІ![]() өД·ҪіМЈ®
өД·ҪіМЈ®
ЈЁ![]() Ј©ТСЦӘ
Ј©ТСЦӘ![]() Ј¬
Ј¬ ![]() ·ЦұрКЗНЦФІ
·ЦұрКЗНЦФІ![]() әНФІ
әНФІ![]() ЙПөД¶ҜөгЈЁ
ЙПөД¶ҜөгЈЁ![]() Ј¬
Ј¬ ![]() О»УЪ
О»УЪ![]() ЦбБҪІаЈ©Ј¬ЗТЦұПЯ
ЦбБҪІаЈ©Ј¬ЗТЦұПЯ![]() Ул
Ул![]() ЦбЖҪРРЈ¬ЦұПЯ
ЦбЖҪРРЈ¬ЦұПЯ![]() Ј¬
Ј¬ ![]() ·ЦұрУл
·ЦұрУл![]() ЦбҪ»УЪөг
ЦбҪ»УЪөг![]() Ј¬
Ј¬ ![]() Ј®ЗуЦӨЈә
Ј®ЗуЦӨЈә ![]() ОӘ¶ЁЦөЈ®
ОӘ¶ЁЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјИэАвЦщ![]() ЦРЈ¬ІаГж
ЦРЈ¬ІаГж![]() ОӘБвРОЈ¬
ОӘБвРОЈ¬ ![]() Ј®
Ј®
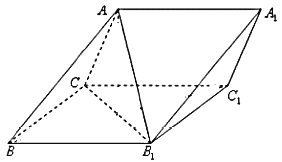
ЈЁ1Ј©ЦӨГчЈә ![]() Ј»
Ј»
ЈЁ2Ј©Иф![]() Ј¬
Ј¬ ![]() Ј¬Зу¶юГжҪЗ
Ј¬Зу¶юГжҪЗ![]() өДУаПТЦөЈ®
өДУаПТЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘНЦФІ![]() өДТ»ёцҪ№өгОӘ
өДТ»ёцҪ№өгОӘ![]() Ј¬ЧуЎўУТ¶Ҙөг·ЦұрОӘ
Ј¬ЧуЎўУТ¶Ҙөг·ЦұрОӘ![]() Ј¬ҫӯ№эөг
Ј¬ҫӯ№эөг![]() ЗТРұВКОӘ
ЗТРұВКОӘ![]() өДЦұПЯ
өДЦұПЯ![]() УлНЦФІ
УлНЦФІ![]() Ҫ»УЪ
Ҫ»УЪ![]() БҪөгЈ®
БҪөгЈ®
ЈЁ1Ј©ЗуНЦФІ![]() өД·ҪіМЈ»
өД·ҪіМЈ»
ЈЁ2Ј©јЗ![]() Ул
Ул![]() өДГж»э·ЦұрОӘ
өДГж»э·ЦұрОӘ![]() әН
әН![]() Ј¬Зу
Ј¬Зу![]() №ШУЪ
№ШУЪ![]() өДұнҙпКҪЈ¬ІўЗуіцөұ
өДұнҙпКҪЈ¬ІўЗуіцөұ![]() ОӘәОЦөКұ
ОӘәОЦөКұ![]() УРЧоҙуЦөЈ®
УРЧоҙуЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
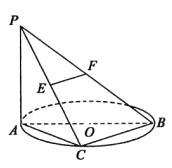
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘ![]() ЛщФЪөДЖҪГжЈ¬
ЛщФЪөДЖҪГжЈ¬ ![]() КЗ
КЗ![]() өДЦұҫ¶Ј¬
өДЦұҫ¶Ј¬ ![]() КЗ
КЗ![]() ЙПТ»өгЈ¬ЗТ
ЙПТ»өгЈ¬ЗТ![]() КЗ
КЗ![]() ЦРөгЈ¬
ЦРөгЈ¬ ![]() ОӘ
ОӘ![]() ЦРөгЈ®
ЦРөгЈ®
ЈЁ1Ј©ЗуЦӨЈә ![]() Гж
Гж![]() Ј»
Ј»
ЈЁ2Ј©ЗуЦӨЈә ![]() Гж
Гж![]() Ј»
Ј»
ЈЁ3Ј©ЗуИэАвЧ¶![]() өДМе»эЈ®
өДМе»эЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝНЦФІ![]() өДАлРДВККЗ
өДАлРДВККЗ![]() Ј¬№эөг
Ј¬№эөг![]() өД¶ҜЦұПЯ
өД¶ҜЦұПЯ![]() УлНЦФІПаҪ»УЪ
УлНЦФІПаҪ»УЪ![]() БҪөгЈ¬өұЦұПЯ
БҪөгЈ¬өұЦұПЯ![]() Ул
Ул![]() ЦбЖҪРРКұЈ¬ЦұПЯ
ЦбЖҪРРКұЈ¬ЦұПЯ![]() ұ»НЦФІ
ұ»НЦФІ![]() ҪШөГөДПЯ¶ОіӨОӘ
ҪШөГөДПЯ¶ОіӨОӘ![]() .
.
ЈЁўсЈ©ЗуНЦФІ![]() өД·ҪіМЈ»
өД·ҪіМЈ»
ЈЁўтЈ©ФЪ![]() ЦбЙПКЗ·сҙжФЪТмУЪөг
ЦбЙПКЗ·сҙжФЪТмУЪөг![]() өД¶Ёөг
өД¶Ёөг![]() Ј¬К№өГЦұПЯ
Ј¬К№өГЦұПЯ![]() ұд»ҜКұЈ¬ЧЬУР
ұд»ҜКұЈ¬ЧЬУР![]() ЈҝИфҙжФЪЈ¬Зуіцөг
ЈҝИфҙжФЪЈ¬Зуіцөг![]() өДЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙ.
өДЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘfЎдЈЁxЈ©КЗәҜКэfЈЁxЈ©өДөјәҜКэЈ¬fЈЁxЈ©өДНјПуИзНјЛщКҫЈ¬ФтІ»өИКҪfЎдЈЁxЈ©fЈЁxЈ©Јј0өДҪвјҜОӘЈЁ Ј© 
A.ЈЁ1Ј¬2Ј©ЎИЈЁ ![]() Ј¬3Ј©ЎИЈЁ©ҒЎЮЈ¬©Ғ1Ј©
Ј¬3Ј©ЎИЈЁ©ҒЎЮЈ¬©Ғ1Ј©
B.ЈЁ©ҒЎЮЈ¬©Ғ1Ј©ЎИЈЁ ![]() Ј¬3Ј©
Ј¬3Ј©
C.ЈЁ©ҒЎЮЈ¬©Ғ1Ј©ЎИЈЁ3Ј¬+ЎЮЈ©
D.ЈЁ1Ј¬2Ј©
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЛ«ЗъПЯ![]() өДҪ№өгКЗНЦФІ
өДҪ№өгКЗНЦФІ![]() Јә
Јә ![]() өД¶ҘөгЈ¬
өД¶ҘөгЈ¬ ![]() ОӘНЦФІ
ОӘНЦФІ![]() өДЧуҪ№өгЗТНЦФІ
өДЧуҪ№өгЗТНЦФІ![]() ҫӯ№эөг
ҫӯ№эөг .
.
ЈЁ1Ј©ЗуНЦФІ![]() өД·ҪіМЈ»
өД·ҪіМЈ»
ЈЁ2Ј©№эНЦФІ![]() өДУТ¶ҘөгЧчРұВКОӘ
өДУТ¶ҘөгЧчРұВКОӘ![]() ЈЁ
ЈЁ![]() Ј©өДЦұПЯҪ»НЦФІ
Ј©өДЦұПЯҪ»НЦФІ![]() УЪБнТ»өг
УЪБнТ»өг![]() Ј¬Б¬Ҫб
Ј¬Б¬Ҫб![]() ІўСУіӨ
ІўСУіӨ![]() Ҫ»НЦФІ
Ҫ»НЦФІ![]() УЪөг
УЪөг![]() Ј¬өұ
Ј¬өұ![]() өДГж»эИЎөГЧоҙуЦөКұЈ¬Зу
өДГж»эИЎөГЧоҙуЦөКұЈ¬Зу![]() өДГж»э.
өДГж»э.
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com