
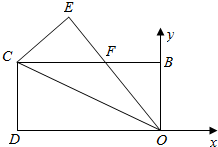
分析 由已知得OE=OD=8,tan∠COD=$\frac{1}{2}$,从而得到tan∠EOD=tan2∠COD=$\frac{4}{3}$,由此能求出E点坐标.
解答  解:∵长方形OBCD沿对角线OC折叠,OD=8,OB=4,
解:∵长方形OBCD沿对角线OC折叠,OD=8,OB=4,
∴OE=OD=8,tan∠COD=$\frac{CD}{OD}$=$\frac{OB}{OD}$=$\frac{4}{8}=\frac{1}{2}$,
∴tan∠EOD=tan2∠COD=$\frac{2tan∠COD}{1-td{n}^{2}∠COD}$=$\frac{2×\frac{1}{2}}{1-(\frac{1}{2})^{2}}$=$\frac{4}{3}$,
∴设E(-4t,-3t),t>0,
∴|-4t|2+|-3t|2=64,解得t=$\frac{8}{5}$,
∴E(-$\frac{32}{5}$,-$\frac{24}{5}$).
点评 本题考查点的坐标的求法,是基础题,解题时要注意正切二倍角定理和长方形折叠性质的合理运用.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:选择题
| A. | (-5,-3) | B. | (-2,-$\frac{3}{2}$ ) | C. | (-$\frac{3}{2}$,-1)? | D. | (-1,-$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
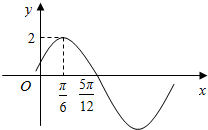 函数f(x)=Asin(ωx+φ)(其中A>0,$|\begin{array}{l}{φ}\end{array}|<\frac{π}{2}$)的图象如图所示,为了得到g(x)=2sin2x的图象,则只需将f(x)的图象( )
函数f(x)=Asin(ωx+φ)(其中A>0,$|\begin{array}{l}{φ}\end{array}|<\frac{π}{2}$)的图象如图所示,为了得到g(x)=2sin2x的图象,则只需将f(x)的图象( )| A. | 向右平移$\frac{π}{6}$个长度单位 | B. | 向右平移$\frac{π}{12}$个长度单位 | ||
| C. | 向左平移$\frac{π}{6}$个长度单位 | D. | 向左平移$\frac{π}{12}$个长度单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
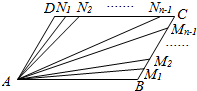 如图,已知平行四边形ABCD,点M1,M2,M3,…,Mn-1和N1,N2,N3,…,Nn-1分别将线段BC和DCn等分(n∈N*,n≥2),若$\overrightarrow{A{M}_{1}}$$+\overrightarrow{A{M}_{2}}$+…$+\overrightarrow{A{M}_{n-1}}$+$\overrightarrow{A{N}_{1}}$$+\overrightarrow{A{N}_{2}}$+…$+\overrightarrow{A{N}_{n-1}}$=30$\overrightarrow{AC}$,则n=( )
如图,已知平行四边形ABCD,点M1,M2,M3,…,Mn-1和N1,N2,N3,…,Nn-1分别将线段BC和DCn等分(n∈N*,n≥2),若$\overrightarrow{A{M}_{1}}$$+\overrightarrow{A{M}_{2}}$+…$+\overrightarrow{A{M}_{n-1}}$+$\overrightarrow{A{N}_{1}}$$+\overrightarrow{A{N}_{2}}$+…$+\overrightarrow{A{N}_{n-1}}$=30$\overrightarrow{AC}$,则n=( )| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
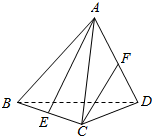 如图所示,ABCD是一个正四面体,E、F分别为BC和AD的中点.
如图所示,ABCD是一个正四面体,E、F分别为BC和AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-4,4] | B. | (-4,4) | C. | [-4,0)∪(0,4] | D. | (-∞,4)∪(4,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com