
【题目】已知圆C:(x+![]() )2+y2=16,点A(
)2+y2=16,点A(![]() ,0),Q是圆上一动点,AQ的垂直平分线交CQ于点M,设点M的轨迹为E.
,0),Q是圆上一动点,AQ的垂直平分线交CQ于点M,设点M的轨迹为E.
(1)求轨迹E的方程;
(2)过点P(1,0)的直线![]() 交轨迹E于两个不同的点A,B,△AOB(O是坐标原点)的面积S=
交轨迹E于两个不同的点A,B,△AOB(O是坐标原点)的面积S=![]() ,求直线AB的方程.
,求直线AB的方程.
【答案】(1) ![]() +y2=1. (2)x+y-1=0或x-y-1=0.
+y2=1. (2)x+y-1=0或x-y-1=0.
【解析】试题分析:(1)由垂直平分线上的点到两端点的距离相等,所以|MC|+|MA|=|MC|+|MQ|=|CQ|=4>2![]() ,即M点的轨迹是椭圆。(2)由(1)得椭圆方程
,即M点的轨迹是椭圆。(2)由(1)得椭圆方程![]() +y2=1,直线斜率存在,所以设直线方程为x=my+1,由面积公式S=
+y2=1,直线斜率存在,所以设直线方程为x=my+1,由面积公式S=![]() |OP||y1-y2|=
|OP||y1-y2|=![]() 及韦达定理可解。
及韦达定理可解。
试题解析:(1)由题意|MC|+|MA|=|MC|+|MQ|=|CQ|=4>2![]() ,
,
所以轨迹E是以A,C为焦点,长轴长为4的椭圆,
即轨迹E的方程为![]() +y2=1.
+y2=1.
(2)记A(x1,y1),B(x2,y2),由题意,直线AB的斜率不可能为0,
而直线x=1也不满足条件,故可设AB的方程为x=my+1.
由![]() 消去x得(4+m2)y2+2my-3=0,
消去x得(4+m2)y2+2my-3=0,
所以 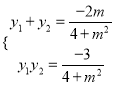
S=![]() |OP||y1-y2|=
|OP||y1-y2|=![]() =
=![]()
由S=![]() ,解得m2=1,即m=±1.
,解得m2=1,即m=±1.
故直线AB的方程为x=±y+1,
即x+y-1=0或x-y-1=0为所求.


科目:高中数学 来源: 题型:
【题目】甲、乙两地相距500千米,一辆货车从甲地行驶到乙地,规定速度不得超过100千米![]() 小时.已知货车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度
小时.已知货车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度![]() (千米
(千米![]() 时)的平方成正比,比例系数为0.01;固定部分为
时)的平方成正比,比例系数为0.01;固定部分为![]() 元(
元(![]() ).
).
(1)把全程运输成本![]() (元)表示为速度
(元)表示为速度![]() (千米
(千米![]() 时)的函数,并指出这个函数的定义域;
时)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个车间为了规定工时定额,需要确定加工某种零件所花费的时间,为此进行了6次试验,收集数据如下:
零件数 |
|
|
|
|
|
|
加工时间 |
|
|
|
|
|
|
(Ⅰ)在给定的坐标系中划出散点图,并指出两个变量是正相关还是负相关;
(Ⅱ)求回归直线方程;
(Ⅲ)试预测加工![]() 个零件所花费的时间?
个零件所花费的时间?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:

 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() ,直线l:
,直线l:![]() (其中
(其中![]() ).
).
(Ⅰ)求直线l所经过的定点P的坐标;
(Ⅱ)若分别过A,B且斜率为![]() 的两条平行直线截直线l所得线段的长为
的两条平行直线截直线l所得线段的长为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知两条公路![]() 的交汇点
的交汇点![]() 处有一学校,现拟在两条公路之间的区域内建一工厂
处有一学校,现拟在两条公路之间的区域内建一工厂![]() ,在两公路旁
,在两公路旁![]() (异于点
(异于点![]() )处设两个销售点,且满足
)处设两个销售点,且满足![]() ,
,![]() (千米),
(千米),![]() (千米),设
(千米),设![]() .
.

(1)试用![]() 表示
表示![]() ,并写出
,并写出![]() 的范围;
的范围;
(2)当![]() 为多大时,工厂产生的噪声对学校的影响最小(即工厂与学校的距离最远).
为多大时,工厂产生的噪声对学校的影响最小(即工厂与学校的距离最远).
(注:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测量中得到的A样本数据如下:52,54,54,56,56,56,55,55,55,55.若B样本数据恰好是A样本数据都加6后所得数据,则A,B两样本的下列数字特征对应相同的是( )
A. 众数 B. 平均数
C. 中位数 D. 标准差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com