
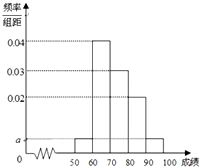
 某校100名学生期末考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期末考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].分析 (1)由频率分布直方图中小矩形面积之和为1,能求出a的值.
(2)由频率分布直方图,能估计这100名学生语文成绩的平均分.
(3)成绩在[50,60)的学生有5人,其中男生比女生多一人,故有3名男生,2名女生,由此能求出从中任选2人此2人都是男生的概率.
解答 解:(1)由频率分布直方图的性质知:
(a+0.04+0.03+0.02+a)×10=1,
解得a=0.005.
(2)由频率分布直方图,估计这100名学生语文成绩的平均分为:
$\overline{x}$=55×0.005×10+65×0.04×10+75×0.03×10+85×0.02×10+95×0.005×10=73.
(3)成绩在[50,60)的学生有0.005×10×100=5人,
其中男生比女生多一人,故有3名男生,2名女生,
从这两名学生中选2人,基本事件总数n=${C}_{5}^{2}$=10,
选中2名男生包含的基本事件个数m=${C}_{3}^{2}$=3,
∴此2人都是男生的概率p=$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$=$\frac{3}{10}$.
点评 本题考查频率分布表的应用,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高二理下学期期末考试数学试卷(解析版) 题型:选择题
设函数f(x),g(x)在[A,B]上均可导,且f′(x)<g′(x),则当A<x<B时,有( )
A.f(x)>g(x)
B.f(x)+g(A)<g(x)+f(A)
C.f(x)<g(x)
D.f(x)+g(B)<g(x)+f(B)
查看答案和解析>>
科目:高中数学 来源:2015-2016学年吉林省高一下学期期末联考数学试卷(解析版) 题型:选择题
已知各项均为正数的数列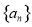 ,其前n项和为
,其前n项和为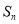 ,且
,且 成等差数列,则数列
成等差数列,则数列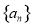 的通项公式为( )
的通项公式为( )
A.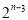 B.
B.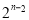 C.
C.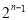 D.
D.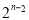 +1
+1
查看答案和解析>>
科目:高中数学 来源:2015-2016学年吉林省高一下学期期末联考数学试卷(解析版) 题型:选择题
已知直线 、
、 , 平面α,
, 平面α,  ∥
∥ ,
,  ∥α, 那么
∥α, 那么 与平面α的关系是( ).
与平面α的关系是( ).
A. ∥α
∥α
B.
 α
α
C. ∥α或
∥α或
 α
α
D. 与α相交
与α相交
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com