练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．二次函数y=ax2+bx+c（a＞0）的图象是抛物线，其焦点到准线的距离是1，则a的值是$\frac{1}{2}$．

    分析 二次函数y=ax2+bx+c可化为y=a（x+$\frac{b}{2a}$）2-$\frac{{b}^{2}}{4a}$+c，形状与y=ax2相似，利用焦点到准线的距离是1，可得$\frac{1}{2a}$=1，即可求出a的值．

    解答 解：二次函数y=ax2+bx+c可化为y=a（x+$\frac{b}{2a}$）2-$\frac{{b}^{2}}{4a}$+c，形状与y=ax2相似，
    ∵焦点到准线的距离是1，∴$\frac{1}{2a}$=1，
    ∴a=$\frac{1}{2}$．
    故答案为：$\frac{1}{2}$．

    点评 本题考查抛物线方程与性质，考查学生的计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    5．已知偶函数f（x）满足，f（x+1）=-f（x）且当x∈[-1，0]时，f（x）=x2，若在区间[-1，3]内，函数g（x）=f（x）-loga（x+2）有4个零点，则实数a的取值范围是[5，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．在正方体OADB-CA′D′B′中，点E是AB与OD的交点，M是OD′与CE的交点，
    （1）试分别用向量$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$表示向量$\overrightarrow{OD′}$和$\overrightarrow{OM}$；
    （2）$\overrightarrow{OI}$，$\overrightarrow{OJ}$，$\overrightarrow{OK}$分别为$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$方向上的单位向量，试用$\overrightarrow{OI}$，$\overrightarrow{OJ}$，$\overrightarrow{OK}$表示$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知圆M与x轴相切且过点（0，2），直线l的参数方程为$\left\{\begin{array}{l}{x=1+t}\\{y=2+\sqrt{3}t}\end{array}\right.$（t为参数）．
    （1）写出直线l的普通方程与圆M的圆心的轨迹方程；
    （2）P为直线l上任意一点，Q为C上的任意一点，求P、Q两点间距离的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知sinα+cosα=$\frac{4}{5}$，且$\frac{3π}{2}$＜α＜2π，计算：
    （1）sinα-cosα；
    （2）$\frac{1}{co{s}^{2}α}$-$\frac{1}{si{n}^{2}α}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知数列{an}的前n项和为Sn=pn2-n（p∈R，且p≠0），且a2，a3，a5依次成等比数列．
    （1）求数列{an}的通项；
    （2）若数列{bn}满足bn=n•2${\;}^{{a}_{n}}$，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知x+2y=2，则$\sqrt{{x}^{2}+{y}^{2}}$+y的最小值为$\frac{\sqrt{155}}{10}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知向量$\overrightarrow{a}$=（3，1），$\overrightarrow{b}$=（2，-1），点O为坐标原点，若向量$\overrightarrow{OA}=3\overrightarrow{a}-\overrightarrow{b}$，$\overrightarrow{BA}=2\overrightarrow{b}-\overrightarrow{a}$，求向量$\overrightarrow{BO}$的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

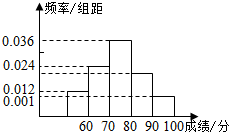    5．对某班的全体学生一次数学测试成绩进行分析，数据的分组情况为：[50，60）[60，70）[70，80）[80，90）[90，100），频率分布直方图如图：
    （Ⅰ）求成绩落在[80，90）之间的频率；
    （Ⅱ）若低于60分的人数是6人，则该班学生人数是多少？
    （Ⅲ）请你估计全班的平均分．

    查看答案和解析>>

    同步练习册答案