
【题目】某种产品的广告费支出![]() 与销售额
与销售额![]() (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求回归直线方程;
(2)试预测广告费支出为![]() 万元时,销售额多大?
万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过![]() 的概率.(参考数据:
的概率.(参考数据: 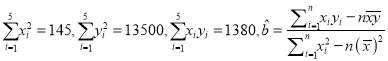 .
.
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时, ![]() ).
).
(1)当![]() 时,求
时,求![]() 的解析式;
的解析式;
(2)若![]() ,试判断
,试判断![]() 的上单调性,并证明你的结论;
的上单调性,并证明你的结论;
(3)是否存在![]() ,使得当
,使得当![]() 时,
时, ![]() 有最大值
有最大值![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个结论:
(1)如果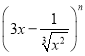 的展开式中各项系数之和为128,则展开式中
的展开式中各项系数之和为128,则展开式中![]() 的系数是-21;
的系数是-21;
(2)用相关指数![]() 来刻画回归效果,
来刻画回归效果, ![]() 的值越大,说明模型的拟合效果越差;
的值越大,说明模型的拟合效果越差;
(3)若![]() 是
是![]() 上的奇函数,且满足
上的奇函数,且满足![]() ,则
,则![]() 的图象关于
的图象关于![]() 对称;
对称;
(4)一个篮球运动员投篮一次得3分的概率为![]() ,得2分的概率为
,得2分的概率为![]() ,不得分的概率为
,不得分的概率为![]() ,且
,且![]() ,已知他投篮一次得分的数学期望为2,则
,已知他投篮一次得分的数学期望为2,则![]() 的最小值为
的最小值为![]() ;
;
其中正确结论的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍。设购进A掀电脑x台,这100台电脑的销售总利润为y元。
①求y与x的关系式;
②该商店购进A型、B型各多少台,才能使销售利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台。若商店保持两种电脑的售价不变,请你以上信息及(2)中的条件,设计出使这100台电脑销售总利润最大的进货方案。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医药研究所开发一种新药,在试验药效时发现:如果成人按规定剂量服用,那么服药后每毫升血液中的含药量y(微克)与时间x(小时)之间满足y= 其对应曲线(如图所示)过点
其对应曲线(如图所示)过点![]() .
.

(1)试求药量峰值(y的最大值)与达峰时间(y取最大值时对应的x值);
(2)如果每毫升血液中含药量不少于1微克时治疗疾病有效,那么成人按规定剂量服用该药后一次能维持多长的有效时间(精确到0.01小时)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com