练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在矩形中，，，是的中点，以为折痕将向上折起，变为，且平面平面.

    （1）求三棱锥的体积；

    （2）求证：；

    （3）求证：平面平面

    【答案】（1）（2）证明见解析（3）证明见解析

    【解析】

    （1）取的中点,连接,可证得平面，且，求出的值，由可得答案；

    （2）由（1）得平面，可得，由已知可得，可得平面，可得，即；

    （2）由（2）得，，且，可得平面，可得平面平面.

    解：（1）取的中点,连接,由是的中点，

    易得为等腰直角三角形，即为等腰直角三角形，且

    由，可得，

    由平面平面，且,平面平面,且 平面，可得平面，

    可得：,

    （2）证明：易得, ,

    可得：, ,

    由（1）得平面，可得，

    由，平面，，平面，

    可得：平面，可得，即.

    (3)由（2）得，，且，且,且平面，平面，可得平面，由平面，

    可得：平面平面.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）若函数在区间上单调递减，试探究函数在区间上的单调性；

    （2）证明：方程在上有且仅有两解.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在如图如示的多面体中，平面平面，四边形是边长为的正方形， ∥,且.

    （1）若分别是中点，求证： ∥平面

    （2）求此多面体的体积

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线的参数方程为 (为参数)，以为极点，以轴的正半轴为极轴，建立极坐标系，直线的极坐标方程为

    （1）求曲线的普通方程和直线的直角坐标方程；

    （2）设点，若直线与曲线相交于，两点，且，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若，证明：曲线在处的切线与直线垂直；

    （2）若，当时，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知一动圆P与定圆外切，且与直线相切，记动点P的轨迹为曲线E．

    （1）求曲线E的方程；

    （2）过点作直线l与曲线E交于不同的两点B、C，设BC中点为Q，问：曲线E上是否存在一点A，使得恒成立？如果存在，求出点A的坐标；如果不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】新闻出版业不断推进供给侧结构性改革，深入推动优化升级和融合发展，持续提高优质出口产品供给，实现了行业的良性发展.下面是2012年至2016年我国新闻出版业和数字出版业营收增长情况，则下列说法错误的是（ ）

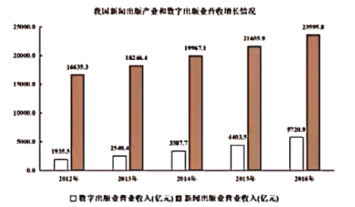
    A. 2012年至2016年我国新闻出版业和数字出版业营收均逐年增加

    B. 2016年我国数字出版业营收超过2012年我国数字出版业营收的2倍

    C. 2016年我国新闻出版业营收超过2012年我国新闻出版业营收的1.5倍

    D. 2016年我国数字出版营收占新闻出版营收的比例未超过三分之一

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知．

    （1）当时，求不等式的解集;

    （2）若时，不等式恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等比数列{an}的前n项和为Sn，a1，公比q>0，S1+a1，S3+a3，S2+a2成等差数列.

    （1）求{an}；

    （2）设bn，求数列{cn}的前n项和Tn.

    查看答案和解析>>

    同步练习册答案