(1)求函数
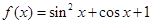
,
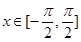
的值域.
(2)求函数
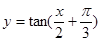
的定义域和单调区间
解:
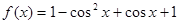
=
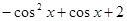
令
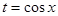
,则
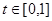
则
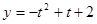
,
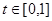
所以当
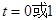
时,
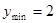
当
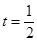
时
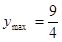
所以
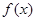
的值域是
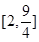
(2)求函数
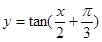
的定义域和单调区间
解:
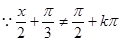
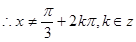
所以
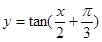
的定义域为

令
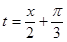
则
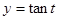
在
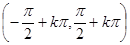
单调递增

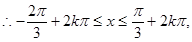
所以
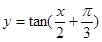
在
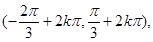
单调递增。
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知函数
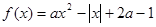
(
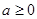
)
(1)若
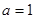
,作出函数
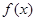
的图象;
(2)设
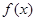
在区间
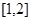
上的最小值为
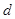
,求
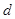
的表达式.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知函数f(x)=ax
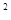
+(1-3a)x+a在区间
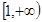
上递增,则实数a的取值范围是__。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分13分)
已知函数
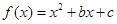
,且
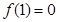
(1)若函数
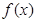
是偶函数,求
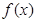
的解析式;
(2)在(1)的条件下,求函数
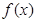
在区间
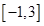
上的最大值和最小值。
(3)要使函数
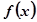
在区间
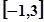
上单调递增,求
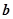
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数

.
(1)若对任意的实数

,都有
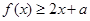
,求

的取值范围;
(2)当

时,
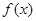
的最大值为M,求证:

;
(3)若

,求证:对于任意的

,
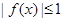
的充要条件是

查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知

-

,求
(1)

时,

的最值。
2.

-1,

时,

的最值。
查看答案和解析>>

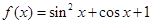 ,
,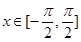 的值域.
的值域.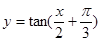 的定义域和单调区间
的定义域和单调区间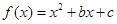 ,且
,且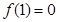
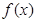 是偶函数,求
是偶函数,求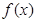 的解析式;
的解析式;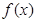 在区间
在区间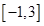 上的最大值和最小值。
上的最大值和最小值。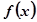 在区间
在区间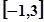 上单调递增,求
上单调递增,求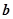 的取值范围.
的取值范围.