
【题目】如图,椭圆C: ![]() =1(a>b>0)的右顶点为A(2,0),左、右焦点分别为F1、F2 , 过点A且斜率为
=1(a>b>0)的右顶点为A(2,0),左、右焦点分别为F1、F2 , 过点A且斜率为 ![]() 的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点F1 .
的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点F1 .
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点P且斜率大于 ![]() 的直线与椭圆交于M,N两点(|PM|>|PN|),若S△PAM:S△PBN=λ,求实数λ的取值范围.
的直线与椭圆交于M,N两点(|PM|>|PN|),若S△PAM:S△PBN=λ,求实数λ的取值范围.
【答案】(Ⅰ)解:因为BF1⊥x轴,得到点 ![]() ,
,
所以  ,所以椭圆C的方程是
,所以椭圆C的方程是 ![]() .
.
(Ⅱ)因为  ,
,
所以 ![]() .由(Ⅰ)可知P(0,﹣1),设MN方程:y=kx﹣1,M(x1,y1),N(x2,y2),
.由(Ⅰ)可知P(0,﹣1),设MN方程:y=kx﹣1,M(x1,y1),N(x2,y2),
联立方程  得:(4k2+3)x2﹣8kx﹣8=0.即得
得:(4k2+3)x2﹣8kx﹣8=0.即得  (*)
(*)
又 ![]() ,有
,有 ![]() ,
,
将 ![]() 代入(*)可得:
代入(*)可得: ![]() .
.
因为 ![]() ,有
,有  ,
,
则 ![]() 且λ>2
且λ>2 ![]() .
.
综上所述,实数λ的取值范围为 ![]() .
.
【解析】(Ⅰ)利用已知条件列出方程组,求解椭圆的几何量,然后求解椭圆C的方程.
(Ⅱ)利用三角形的面积的比值,推出线段的比值,得到 ![]() .设MN方程:y=kx﹣1,M(x1,y1),N(x2,y2),联立方程
.设MN方程:y=kx﹣1,M(x1,y1),N(x2,y2),联立方程  ,利用韦达定理,求出
,利用韦达定理,求出 ![]() ,解出
,解出 ![]() ,将
,将 ![]() 椭圆方程,然后求解实数λ的取值范围.
椭圆方程,然后求解实数λ的取值范围.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
【题目】已知A是双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左顶点,F1 , F2分别为左、右焦点,P为双曲线上一点,G是△F1PF2的重心,若
=1(a>0,b>0)的左顶点,F1 , F2分别为左、右焦点,P为双曲线上一点,G是△F1PF2的重心,若 ![]() =λ
=λ ![]() ,|
,| ![]() |=
|= ![]() ,|
,| ![]() |+|
|+| ![]() |=8,则双曲线的标准方程为( )
|=8,则双曲线的标准方程为( )
A.x2﹣ ![]() =1
=1
B.![]() ﹣y2=1
﹣y2=1
C.![]() =1
=1
D.x2﹣ ![]() =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四面体A﹣BCD中,AB=CD=10,AC=BD=2 ![]() ,AD=BC=2
,AD=BC=2 ![]() ,则四面体A﹣BCD外接球的表面积为( )
,则四面体A﹣BCD外接球的表面积为( )
A.50π
B.100π
C.200π
D.300π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E﹣ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DF的中点. (I)求证:BE∥平面ACF;
(II)求平面BCF与平面BEF所成锐二面角的余弦角.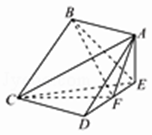
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】体积为 ![]() 的正三棱锥A﹣BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是( )
的正三棱锥A﹣BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是( ) 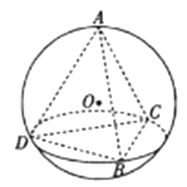
A.[4π,12π]
B.[8π,16π]
C.[8π,12π]
D.[12π,16π]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y= ![]() sin(2x﹣
sin(2x﹣ ![]() )的图象,只需将函数y=sinxcosx的图象( )
)的图象,只需将函数y=sinxcosx的图象( )
A.向左平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线l过定点P(1,1),且倾斜角为 ![]() ,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为 ![]() .
.
(1)求曲线C的直角坐标方程与直线l的参数方程;
(2)若直线l与曲线C相交于不同的两点A,B,求|AB|及|PA||PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】渝州集团对所有员工进行了职业技能测试从甲、乙两部门中各任选10名员工的测试成绩(单位:分)数据的茎叶图如图所示. 
(1)若公司决定测试成绩高于85分的员工获得“职业技能好能手”称号,求从这20名员工中任选三人,其中恰有两人获得“职业技能好能手”的概率;
(2)公司结合这次测试成绩对员工的绩效奖金进行调整(绩效奖金方案如表),若以甲部门这10人的样本数据来估计该部门总体数据,且以频率估计概率,从甲部门所有员工中任选3名员工,记绩效奖金不小于3a的人数为ξ,求ξ的分布列及数学期望.
分数 | [60,70) | [70,80) | [80,90) | [90,100] |
奖金 | a | 2a | 3a | 4a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com