
【题目】安排6名学生去3个社区进行志愿服务,且每人只去一个社区,要求每个社区至少有一名学生进行志愿服务,则不同的安排方式共有( ).
A.360种B.300种C.540种D.180种
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】近来国内一些互联网公司为了赢得更大的利润、提升员工的奋斗姿态,要求员工实行![]() 工作制,即工作日早
工作制,即工作日早![]() 点上班,晚上
点上班,晚上![]() 点下班,中午和傍晚最多休息
点下班,中午和傍晚最多休息![]() 小时,总计工作
小时,总计工作![]() 小时以上,并且一周工作
小时以上,并且一周工作![]() 天的工作制度,工作期间还不能请假,也没有任何补贴和加班费.消息一出,社交媒体一片哗然,有的人认为这是违反《劳动法》的一种对员工的压榨行为,有的人认为只有付出超越别人的努力和时间,才能够实现想要的成功,这是提升员工价值的一种有效方式.对此,国内某大型企业集团管理者认为应当在公司内部实行
天的工作制度,工作期间还不能请假,也没有任何补贴和加班费.消息一出,社交媒体一片哗然,有的人认为这是违反《劳动法》的一种对员工的压榨行为,有的人认为只有付出超越别人的努力和时间,才能够实现想要的成功,这是提升员工价值的一种有效方式.对此,国内某大型企业集团管理者认为应当在公司内部实行![]() 工作制,但应该给予一定的加班补贴(单位:百元),对于每月的补贴数额集团人力资源管理部门随机抽取了集团内部的
工作制,但应该给予一定的加班补贴(单位:百元),对于每月的补贴数额集团人力资源管理部门随机抽取了集团内部的![]() 名员工进行了补贴数额(单位:百元)期望值的网上问卷调查,并把所得数据列成如下所示的频数分布表:
名员工进行了补贴数额(单位:百元)期望值的网上问卷调查,并把所得数据列成如下所示的频数分布表:
组别(单位:百元) |
|
|
|
|
|
频数(人数) |
|
|
|
|
|
(Ⅰ)求所得样本的中位数(精确到百元);
(Ⅱ)根据样本数据,可近似地认为员工的加班补贴X服从正态分布![]() ,若该集团共有员工
,若该集团共有员工![]() ,试估计有多少员工期待加班补贴在
,试估计有多少员工期待加班补贴在![]() 元以上;
元以上;
(Ⅲ)已知样本数据中期望补贴数额在![]() 范围内的
范围内的![]() 名员工中有
名员工中有![]() 名男性,
名男性,![]() 名女性,现选其中
名女性,现选其中![]() 名员工进行消费调查,记选出的女职员人数为
名员工进行消费调查,记选出的女职员人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店每天(开始营业时)以每件15元的价格购入![]() 商品若干(
商品若干(![]() 商品在商店的保鲜时间为8小时,该商店的营业时间也恰好为8小时),并开始以每件30元的价格出售,若前6小时内所购进的
商品在商店的保鲜时间为8小时,该商店的营业时间也恰好为8小时),并开始以每件30元的价格出售,若前6小时内所购进的![]() 商品没有售完,则商店对没卖出的
商品没有售完,则商店对没卖出的![]() 商品将以每件10元的价格低价处理完毕(根据经验,2小时内完全能够把
商品将以每件10元的价格低价处理完毕(根据经验,2小时内完全能够把![]() 商品低价处理完毕,且处理完毕后,当天不再购进
商品低价处理完毕,且处理完毕后,当天不再购进![]() 商品).该商店统计了100天
商品).该商店统计了100天![]() 商品在每天的前6小时内的销售量,由于某种原因销售量频数表中的部分数据被污损而不能看清,制成如下表格(注:视频率为概率).
商品在每天的前6小时内的销售量,由于某种原因销售量频数表中的部分数据被污损而不能看清,制成如下表格(注:视频率为概率).
前6小时内的销售量 (单位:件) | 3 | 4 | 5 |
频数 | 30 |
|
|
(1)若某天商店购进![]() 商品4件,试求商店该天销售
商品4件,试求商店该天销售![]() 商品获取利润
商品获取利润![]() 的分布列和期望;
的分布列和期望;
(2)若商店每天在购进4件![]() 商品时所获得的平均利润最大,求
商品时所获得的平均利润最大,求![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的命题的是( )
A.已知随机变量服从二项分布![]() ,若
,若![]() ,
,![]() ,则
,则![]() ;
;
B.将一组数据中的每个数据都加上同一个常数后,方差恒不变;
C.设随机变量![]() 服从正态分布
服从正态分布![]() ,若
,若![]() ,则
,则![]() ;
;
D.某人在10次射击中,击中目标的次数为![]() ,
,![]() ,则当
,则当![]() 时概率最大.
时概率最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】黄冈市有很多名优土特产,黄冈市的蕲春县就有闻名于世的“蕲春四宝”![]() 蕲竹、蕲艾、蕲蛇、蕲龟
蕲竹、蕲艾、蕲蛇、蕲龟![]() ,很多人慕名而来旅游,通过随机询问60名不同性别的游客在购买“蕲春四宝”时是否在来蕲春县之前就知道“蕲春四宝”,得到如下列联表:
,很多人慕名而来旅游,通过随机询问60名不同性别的游客在购买“蕲春四宝”时是否在来蕲春县之前就知道“蕲春四宝”,得到如下列联表:
男 | 女 | 总计 | |
事先知道“蕲春四宝” | 8 |
|
|
事先不知道“蕲春四宝” |
| 4 | 36 |
总计 | 40 |
|
|
|
|
|
|
|
|
|
|
附:![]()
![]() 写出列联表中各字母代表的数字;
写出列联表中各字母代表的数字;
![]() 由以上列联表判断,能否在犯错误的概率不超过
由以上列联表判断,能否在犯错误的概率不超过![]() 的前提下认为购买“蕲春四宝”和是否“事先知道
的前提下认为购买“蕲春四宝”和是否“事先知道![]() 蕲春四宝
蕲春四宝![]() 有关系”?
有关系”?
![]() 从被询问的
从被询问的![]() 名事先知道“蕲春四宝”的顾客中随机选取2名顾客,求抽到的女顾客人数的分布列及其数学期望.
名事先知道“蕲春四宝”的顾客中随机选取2名顾客,求抽到的女顾客人数的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有某高新技术企业年研发费用投入![]() (百万元)与企业年利润
(百万元)与企业年利润![]() (百万元)之间具有线性相关关系,近5年的年研发费用和年利润的具体数据如表:
(百万元)之间具有线性相关关系,近5年的年研发费用和年利润的具体数据如表:
年研发费用 |
|
|
|
|
|
年利润 |
|
|
|
|
|
数据表明![]() 与
与![]() 之间有较强的线性关系.
之间有较强的线性关系.
(1)求![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(2)如果该企业某年研发费用投入8百万元,预测该企业获得年利润为多少?
参考数据:回归直线的系数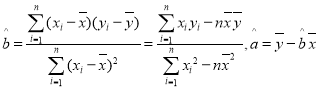 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com