
【题目】某高中志愿者部有男志愿者6人,女志愿者4人,这些人要参加元旦联欢会的服务工作. 从这些人中随机抽取4人负责舞台服务工作,另外6人负责会场服务工作.
(Ⅰ)设![]() 为事件:“负责会场服务工作的志愿者中包含女志愿者
为事件:“负责会场服务工作的志愿者中包含女志愿者![]() 但不包含男志愿者
但不包含男志愿者![]() ”,求事件
”,求事件![]() 发生的概率.
发生的概率.
(Ⅱ)设![]() 表示参加舞台服务工作的女志愿者人数,求随机变量
表示参加舞台服务工作的女志愿者人数,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,离心率为
,离心率为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() 的周长为
的周长为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 分别交于
分别交于![]() 两点,且
两点,且![]() ,试问点
,试问点![]() 到直线
到直线![]() 的距离是否为定值,证明你的结论.
的距离是否为定值,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产A、B两种产品,根据市场调查,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的平方根成正比,其关系如图2(注:单位是万元).


图1 图2
(1)若A、B两种产品的利润表示为投资的函数分别为![]() 、
、![]() ,求出它们的表达式并注明定义域;
,求出它们的表达式并注明定义域;
(2)现企业有20万元资金全部投入A、B两种产品的生产,问:怎样分配这20万元资金,能使获得的利润最大,其最大利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
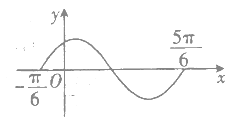
【题目】如图所示的是函数![]() (
(![]() ,
,![]() )在区间
)在区间![]() 上的图象,将该函数图象各点的横坐标缩小到原来的一半(纵坐标不变),再向右平移
上的图象,将该函数图象各点的横坐标缩小到原来的一半(纵坐标不变),再向右平移![]() (
(![]() )个单位长度后,所得到的图象关于直线
)个单位长度后,所得到的图象关于直线![]() 对称,则
对称,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
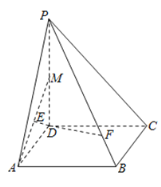
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 底面ABCD,且
底面ABCD,且![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() :
:![]() 上一点,且
上一点,且![]() 到
到![]() 的焦点的距离为
的焦点的距离为![]() .
.
(1)若直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,证明:
为坐标原点,证明:![]() ;
;
(2)若![]() 是
是![]() 上一动点,点
上一动点,点![]() 不在直线
不在直线![]() :
:![]() 上,过
上,过![]() 作直线垂直于
作直线垂直于![]() 轴且交
轴且交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() .试判断
.试判断![]() 与
与![]() 中是否有一个为定值?若是,请指出哪一个为定值,并加以证明;若不是,请说明理由.
中是否有一个为定值?若是,请指出哪一个为定值,并加以证明;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品企业一个月内被消费者投诉的次数用![]() 表示,据统计,随机变量
表示,据统计,随机变量![]() 的概率分布如列联表.
的概率分布如列联表.
|
|
|
|
|
|
|
|
|
|
(1)求![]() 的值和
的值和![]() 的数学期望;
的数学期望;
(2)假设一月份与二月份被消费者投诉的次数互不影响求该企业在这两个月内共被消费者投诉![]() 次的概率.
次的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com