
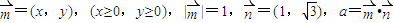 ,则
,则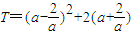 的最大值为( )
的最大值为( )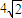
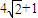
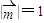 ,x≥0,y≥0
,x≥0,y≥0 ,
,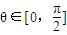 ,又
,又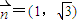 ,
,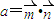 =
=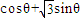 =
=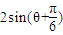 ,
,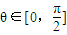
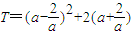 =
=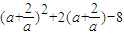 =
=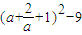
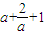 ∈[
∈[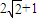 ,4]
,4]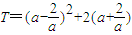 的最大值为16-9=7
的最大值为16-9=7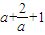 在a∈[1,2]上的单调性求出最值,本题涉及到了向量三角,函数的单调性,涉及到的考点多,综合性强,考查了转化的思想及根据题设条件灵活选择解题的方法的能力.
在a∈[1,2]上的单调性求出最值,本题涉及到了向量三角,函数的单调性,涉及到的考点多,综合性强,考查了转化的思想及根据题设条件灵活选择解题的方法的能力. 

 全能测控一本好卷系列答案
全能测控一本好卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com