
【题目】1772年德国的天文学家波得发现了求太阳的行星距离的法则,记地球距离太阳的平均距离为10,可以算得当时已知的六大行星距离太阳的平均距离如下表:
星名 | 水星 | 金星 | 地球 | 火星 | 木星 | 土星 |
与太阳的距离 | 4 | 7 | 10 | 16 | 52 | 100 |
除水星外,其余各星与太阳的距离都满足波得定则(某一数列规律),当时德国数学家高斯根据此定则推算,火星和木星之间距离太阳28还有一颗大行星,1801年,意大利天文学家皮亚齐经过观测,果然找到了火星和木星之间距离太阳28的谷神星以及它所在的小行星带,请你根据这个定则,估算从水星开始由近到远算,第10个行星与太阳的平均距离大约是( )
A.388B.772C.1540D.3076
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,若函数
时,若函数![]() 在
在![]() ,
,![]() (
(![]() )处导数相等,证明:
)处导数相等,证明:![]() ;
;
(2)是否存在![]() ,使直线
,使直线![]() 是曲线
是曲线![]() 的切线,也是曲线
的切线,也是曲线![]() 的切线,而且这样的直线
的切线,而且这样的直线![]() 是唯一的,如果存在,求出直线
是唯一的,如果存在,求出直线![]() 方程,如果不存在,请说明理由.
方程,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有曲池,上中周二丈,外周四丈,广一丈,下中周一丈四尺,外周二丈四尺,广五尺,深一丈,问积几何?”其意思为:“今有上下底面皆为扇形的水池,上底中周2丈,外周4丈,宽1丈;下底中周1丈4尺,外周长2丈4尺,宽5尺;深1丈.问它的容积是多少?”则该曲池的容积为( )立方尺(1丈=10尺,曲池:上下底面皆为扇形的土池,其容积公式为![]() [(2×上宽+下宽)
[(2×上宽+下宽)![]() (2×下宽+上宽)
(2×下宽+上宽)![]() ]×深)
]×深)
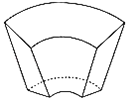
A.![]() B.1890C.
B.1890C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ2﹣4ρsin(θ![]() )=0.
)=0.
(1)求曲线C的直角坐标方程;
(2)若直线l的参数方程是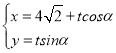 (α为参数),且α∈(
(α为参数),且α∈(![]() ,π)时,直线l与曲线C有且只有一个交点P,求点P的极径.
,π)时,直线l与曲线C有且只有一个交点P,求点P的极径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
:![]() (
(![]() ,
,![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线交双曲线于
的直线交双曲线于![]() ,
,![]() 两点,线段
两点,线段![]() 的垂直平分线恰过点
的垂直平分线恰过点![]() ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点![]() ,焦点在
,焦点在![]() 轴上,离心率为
轴上,离心率为![]() 的椭圆过点
的椭圆过点![]()

(1)求椭圆的方程;
(2)设不过原点![]() 的直线
的直线![]() 与该椭圆交于
与该椭圆交于![]() 两点,满足直线
两点,满足直线![]() 的斜率依次成等比数列,求
的斜率依次成等比数列,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为F
的右焦点为F![]() ,点B是椭圆C的短轴的一个端点,ΔOFB的面积为
,点B是椭圆C的短轴的一个端点,ΔOFB的面积为![]() ,椭圆C上的两点H、G关于原点O对称,且
,椭圆C上的两点H、G关于原点O对称,且![]() 、
、![]() 的等差中项为2
的等差中项为2
(1)求椭圆的方程;
(2)是否存在过点M(2,1)的直线![]() 与椭圆C交于不同的两点P、Q,且使得
与椭圆C交于不同的两点P、Q,且使得![]() 成立?若存在,试求出直线
成立?若存在,试求出直线![]() 的方程;若不存在,请说明理由
的方程;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com