
【题目】【2017重庆二诊】已知函数![]() ,设关于
,设关于![]() 的方程
的方程![]() 有
有![]() 个不同的实数解,则
个不同的实数解,则![]() 的所有可能的值为( )
的所有可能的值为( )
A. 3 B. 1或3 C. 4或6 D. 3或4或6
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
【题目】如图,在四边形ABCD中,△ABC是边长为6的正三角形,设 ![]() (x,y∈R).
(x,y∈R). 
(1)若x=y=1,求| ![]() |;
|;
(2)若 ![]() =36,
=36, ![]() =54,求x,y.
=54,求x,y.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】政府鼓励创新、创业,银行给予低息贷款.一位大学毕业生向自主创业,经过市场调研、测算,有两个方案可供选择.
方案1:开设一个科技小微企业,需要一次性贷款40万元,第一年获利是贷款额的10%,以后每年比上一年增加25%的利润.
方案2:开设一家食品小店,需要一次性贷款20万元,第一年获利是贷款额的15%,以后每年比上一年增加利润1.5万元.两种方案使用期限都是10年,到期一次性还本付息.两种方案均按年息2%的复利计算(参考数据:1.259=7.45,1.2510=9.3,1.029=1.20,1.0210=1.22).
(1)10年后,方案1,方案2的总收入分别有多少万元?
(2)10年后,哪一种方案的利润较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的方程为![]() ,过点
,过点![]() 的一条直线与抛物线
的一条直线与抛物线![]() 交于
交于![]() 两点,若抛物线在
两点,若抛物线在![]() 两点的切线交于点
两点的切线交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 与直线
与直线![]() 的夹角为
的夹角为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017福建三明5月质检】已知直线![]() 与抛物线
与抛物线![]() 相切,且与
相切,且与![]() 轴的交点为
轴的交点为![]() ,点
,点![]() .若动点
.若动点![]() 与两定点
与两定点![]() 所构成三角形的周长为6.
所构成三角形的周长为6.
(Ⅰ) 求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ) 设斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,当
两点,当![]() ,且
,且![]() 位于直线
位于直线![]() 的两侧时,证明:
的两侧时,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017安徽阜阳二模】一企业从某生产线上随机抽取![]() 件产品,测量这些产品的某项技术指标值
件产品,测量这些产品的某项技术指标值![]() ,得到的频率分布直方图如图.
,得到的频率分布直方图如图.
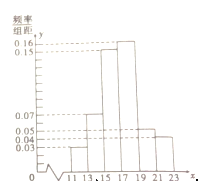
(1)估计该技术指标值![]() 平均数
平均数![]() ;
;
(2)在直方图的技术指标值分组中,以![]() 落入各区间的频率作为
落入各区间的频率作为![]() 取该区间值的频率,若
取该区间值的频率,若![]() ,则产品不合格,现该企业每天从该生产线上随机抽取
,则产品不合格,现该企业每天从该生产线上随机抽取![]() 件产品检测,记不合格产品的个数为
件产品检测,记不合格产品的个数为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)
设函数![]() .
.
(1)若![]() =1时,函数
=1时,函数![]() 取最小值,求实数
取最小值,求实数![]() 的值;
的值;
(2)若函数![]() 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,证明对任意正整数
,证明对任意正整数![]() ,不等式
,不等式![]() 都成立.
都成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com