
【题目】在某校歌咏比赛中,甲班、乙班、丙班、丁班均可从![]() 、
、![]() 、
、![]() 、
、![]() 四首不同曲目中任选一首.
四首不同曲目中任选一首.
(1)求甲、乙两班选择不同曲目的概率;
(2)设这四个班级总共选取了![]() 首曲目,求
首曲目,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形, ![]() ,四边形
,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() .
.
(1)在图中画出过点![]() 的平面
的平面![]() ,使得
,使得![]() 平面
平面![]() (必须说明画法,不需证明);
(必须说明画法,不需证明);
(2)若二面角![]() 是
是![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的4月23日是“世界读书日”,某校研究性学习小组为了解本校学生的阅读情况,随机调查了本校200名学生在这一天的阅读时间![]() (单位:分钟),将样本数据整理后绘制成如图的样本频率分布直方图.
(单位:分钟),将样本数据整理后绘制成如图的样本频率分布直方图.
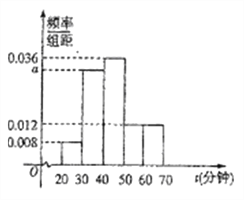
(1)求![]() 的值;
的值;
(2)试估计该学校所有学生在这一天的平均阅读时间;
(3)若用分层抽样的方法从这200名学生中,抽出25人参加交流会,则阅读时间为![]() ,
, ![]() 的两组中各抽取多少人?
的两组中各抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十二届全国人民代表大会第五次会议和政协第十二届全国委员会第五次会议(简称两会)将分别于2017年3月5日和3月3日在北京开幕,某高校学生会为了解该校学生对全国两会的关注情况,随机调查了该校200名学生,并将这200名学生分为对两会“比较关注”与“不太关注”两类,已知这200名学生中男生比女生多20人,对两会“比较关注”的学生中男生人数与女生人数之比为![]() ,对两会“不太关注”的学生中男生比女生少5人.
,对两会“不太关注”的学生中男生比女生少5人.
(1)完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为男生与女生对两会的关注有差异?
的把握认为男生与女生对两会的关注有差异?
比较关注 | 不太关注 | 合计 | |
男生 | |||
女生 | |||
合计 |
(2)该校学生会从对两会“比较关注”的学生中根据性别进行分层抽样,从中抽取7人,再从这7人中随机选出2人参与两会宣传活动,求这2人全是男生的概率.
附:![]() ,
,![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中AD∥BC,∠ADC=90°,平面ABCD外一点P在平面ABCD内的射影Q恰在边AD上, PA=AD=2 BC=2,CD=.
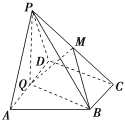
(1)若平面PQB⊥平面PAD,求证:Q为线段AD中点;
(2)在(1)的条件下,若M在线段PC上,且PA∥平面BMQ,求点M到平面PAB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是偶函数,定义x≥0时,f(x)= ![]()
(1)求f(﹣2);
(2)当x<﹣3时,求f(x)的解析式;
(3)设函数y=f(x)在区间[﹣5,5]上的最大值为g(a),试求g(a)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了![]() 人,得到如下的统计表和频率分布直方图.
人,得到如下的统计表和频率分布直方图.
(1)写出其中的![]() 、
、![]() 、
、![]() 及
及![]() 和
和![]() 的值;
的值;
(2)若从第1,2,3组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人,求这三组每组分别抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求这2人都是第3组的概率

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (a>0,a≠1).
(a>0,a≠1).
(1)判断函数f(x)的奇偶性;
(2)判断函数f(x)在(1,+∞)上的单调性,并给出证明;
(3)当x∈(n,a﹣2)时,函数f(x)的值域是(1,+∞),求实数a与n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com