
【题目】椭圆![]()
![]() 的离心率为
的离心率为![]() ,其右焦点到点
,其右焦点到点![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 不是左右顶点),且以
不是左右顶点),且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 的右顶点,求证直线
的右顶点,求证直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
【答案】(1)![]() ;(2)证明见解析,
;(2)证明见解析,![]()
【解析】
(1)由右焦点到点![]() 的距离为
的距离为![]() 得到
得到![]() ,解出
,解出![]() ,由椭圆离心率为
,由椭圆离心率为![]() ,得到
,得到![]() ,解出
,解出![]() ,由
,由![]() ,即可求得椭圆方程;
,即可求得椭圆方程;
(2)记椭圆右顶点为点![]() ,设
,设![]() ,
,![]() ,联立直线
,联立直线![]() 与椭圆
与椭圆![]() 方程,消去
方程,消去![]() 并整理,由韦达定理得到根与系数的关系,再利用以AB为直径的圆过椭圆的右顶点,可得
并整理,由韦达定理得到根与系数的关系,再利用以AB为直径的圆过椭圆的右顶点,可得![]() ,化简整理可得
,化简整理可得![]() 与
与![]() 的关系,可证直线
的关系,可证直线![]() 过定点,求出该定点的坐标即可.
过定点,求出该定点的坐标即可.
解:(1)![]() 右焦点
右焦点![]() 到点
到点![]() 的距离为
的距离为![]() ,
,
![]()
 ,解得
,解得![]() ,
,
又![]() 椭圆
椭圆![]()
![]() 的离心率为
的离心率为![]() ,
,
![]()
![]() ,解得
,解得![]() ,
,
![]()
![]() ,
,
![]() 所求椭圆C的标准方程为
所求椭圆C的标准方程为![]() .
.
(2)记椭圆右顶点为点![]() ,则
,则![]() ,
,
设![]() ,
,![]() ,
,
联立直线![]() 与椭圆
与椭圆![]() 方程,得
方程,得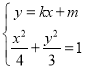 ,
,
消去![]() 得
得![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 以AB为直径的圆过椭圆的右顶点
以AB为直径的圆过椭圆的右顶点![]() ,
,
![]()
![]() ,即
,即![]() ,
,
又![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
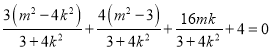 ,
,
整理得![]() ,
,
解得![]() ,均满足
,均满足![]() ,
,
当![]() 时,
时,![]() :
:![]() ,直线过定点(2,0),与已知矛盾,
,直线过定点(2,0),与已知矛盾,
当![]() 时,
时, ![]() :
:![]() ,直线过定点
,直线过定点![]() ,
,
综上所述,直线![]() 过定点,定点坐标为
过定点,定点坐标为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 底面
底面![]() ,
,![]() ,E为线段
,E为线段![]() 的中点.
的中点.
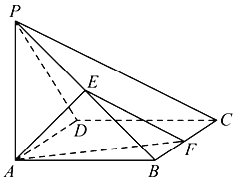
(1)证明:点F在线段![]() 上移动时,
上移动时,![]() 为直角三角形;
为直角三角形;
(2)若F为线段![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)曲线![]() 与曲线
与曲线![]() 有两个公共点,求实数
有两个公共点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:①![]() 使得
使得![]() 成立;②
成立;②![]() ,都有
,都有![]() 成立,是
成立,是![]() 在区间D上单调递增的充要条件;③只要函数有零点,我们就可以用二分法求出零点的近似值;④过点
在区间D上单调递增的充要条件;③只要函数有零点,我们就可以用二分法求出零点的近似值;④过点![]() 作直线,使它与抛物线
作直线,使它与抛物线![]() 仅有一个公共点,这样的直线有2条;正确的个数是( )
仅有一个公共点,这样的直线有2条;正确的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体![]() 中,面
中,面![]() 为矩形,面
为矩形,面![]() 面
面![]() ,
,![]() .
.
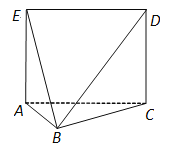
(1)求证:面![]() 面
面![]() ;
;
(2)已知多面体![]() 各顶点均在同一球面上,且该球的表面积为
各顶点均在同一球面上,且该球的表面积为![]() ,
,![]() ,当这个多面体的体积取得最大值时求其侧视图的面积.
,当这个多面体的体积取得最大值时求其侧视图的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新中国成立70周年以来,党中央国务院高度重视改善人民生活,始终把提高人民生活水平作为一切工作的出发点和落脚点城乡居民收入大幅增长,居民生活发生了翻天覆地的变化.下面是1949年及2015年~2018年中国居民人均可支配收入(元)统计图.以下结论中不正确的是( )

A.20l5年-2018年中国居民人均可支配收入与年份成正相关
B.2018年中居民人均可支配收入超过了1949年的500倍
C.2015年-2018年中国居民人均可支配收入平均超过了24000元
D.2015年-2018年中围居民人均可支配收入都超过了1949年的500倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中,由四个全等的直角三角形和一个正方形构成.现有五种不同的颜色可供涂色,要求相邻的区域不能用同一种颜色,则不同的涂色方案有( )
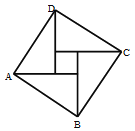
A.180B.192C.420D.480
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com