
| 3 |
| 2 |
| ||
| 2 |
| OM |
| ON |
| x2 |
| a2 |
| y2 |
| b2 |
|
| y2 |
| x |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
|
|
| x2 |
| 4 |
| x2 |
| 4 |
| a2-b2 |
| 3 |
| ||
| 2 |
|
| -2m |
| m2+4 |
| -3 |
| m2+4 |
| -2m |
| m2+4 |
| -3 |
| m2+4 |
| 4-4m2 |
| m2=4 |
| OM |
| ON |
| OM |
| ON |
| 4-4m2 |
| m2+4 |
| -3 |
| m2+4 |
| 1 |
| 2 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
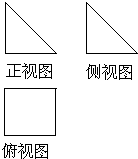 һ�����������ͼ��ͼ��ʾ��������ͼ�Ͳ���ͼ���ǵ���ֱ�������Σ�ֱ�DZ߳�Ϊ1����ü����������ı����Ϊ��������
һ�����������ͼ��ͼ��ʾ��������ͼ�Ͳ���ͼ���ǵ���ֱ�������Σ�ֱ�DZ߳�Ϊ1����ü����������ı����Ϊ��������A��
| ||
| B��2�� | ||
| C��3�� | ||
| D��12�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| a+b |
| 2 |
| ab |
| A����ֲ���Ҫ���� |
| B����Ҫ��������� |
| C����Ҫ���� |
| D���Ȳ���Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
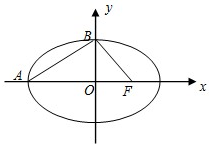 ��֪��ԲC��
��֪��ԲC��| x2 |
| a2 |
| y2 |
| b2 |
| OF |
| FB |
| AB |
| BF |
| FM |
| FN |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 2 |
| OM |
| ON |
| OP |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
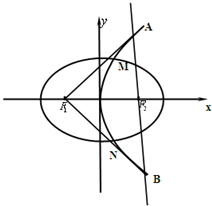 ��֪��ԲC�Ľ���ΪF1��-1��0����F2��1��0������P��-1��
��֪��ԲC�Ľ���ΪF1��-1��0����F2��1��0������P��-1��
| ||
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
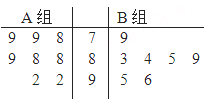 �츮������ս�Զ�λ���Գ���һ�廯��ȫ���ִ���������������ʻ�Ϊ���죬�����ִ�����ҵΪ�����߶˷���ҵ���ۣ���ҵ�����˾ӵĹ��ʻ��ִ��³�����Ϊ�������㳧�ң�ij��ҵ��16�ҳ��Ҹ��ݵ����Ϊ���飬�ֱ���A��B������ί�Ը���ָ������ۺ����ȴ�֣�������Ӷ�16�ҳ�����������ۺϵ÷ֵľ�Ҷͼ��ͼ��ʾ�����о�Ϊʮλ����ҶΪ��λ������ij�����ܺ͵÷ָ���16�ҳ��ҵ�ƽ������ȷ��Ϊ���㳧�ң�
�츮������ս�Զ�λ���Գ���һ�廯��ȫ���ִ���������������ʻ�Ϊ���죬�����ִ�����ҵΪ�����߶˷���ҵ���ۣ���ҵ�����˾ӵĹ��ʻ��ִ��³�����Ϊ�������㳧�ң�ij��ҵ��16�ҳ��Ҹ��ݵ����Ϊ���飬�ֱ���A��B������ί�Ը���ָ������ۺ����ȴ�֣�������Ӷ�16�ҳ�����������ۺϵ÷ֵľ�Ҷͼ��ͼ��ʾ�����о�Ϊʮλ����ҶΪ��λ������ij�����ܺ͵÷ָ���16�ҳ��ҵ�ƽ������ȷ��Ϊ���㳧�ң��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com