
【题目】已知函数f(x)=x2+2alnx.
(1)若函数f(x)的图象在(2,f(2))处的切线斜率为1,求实数a的值;
(2)若函数![]() 在[1,2]上是减函数,求实数a的取值范围.
在[1,2]上是减函数,求实数a的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】随机抽取某校高一100名学生的期末考试英语成绩(他们的英语成绩都在80分![]() 140分之间),将他们的英语成绩(单位:分)分成:
140分之间),将他们的英语成绩(单位:分)分成:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六组,得到如图所示的部分频率分布直方图,已知成绩处于
六组,得到如图所示的部分频率分布直方图,已知成绩处于![]() 内与
内与![]() 内的频数之和等于成绩处于
内的频数之和等于成绩处于![]() 内的频数,根据图中的信息,回答下列问题:
内的频数,根据图中的信息,回答下列问题:
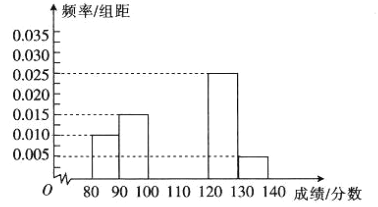
(1)求频率分布直方图中未画出的小矩形的面积之和;
(2)求成绩处于![]() 内与
内与![]() 内的频率之差;
内的频率之差;
(3)用分层抽样的方法从成绩不低于120分的学生中选取一个容量为6的样本,将该样本看成一个总体,从中任选2人,求这2人中恰有一人成绩低于130分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行六面体ABCD—A1B1C1D1中,AB=AC,平面BB1C1C⊥底面ABCD,点M、F分别是线段AA1、BC的中点.
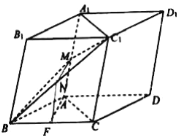
(1)求证:AF⊥DD1;
(2)求证:AF∥平面MBC1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上有n个点,任意三点不共线,任意两点之间连一条线段,并将每条线段染为红色与蓝色之一,称三边颜色相同的三角形为“同色三角形”.记同色三角形的个数为S.
(1)若![]() ,对于所有可能的染法,求S的最小值;
,对于所有可能的染法,求S的最小值;
(2)若![]() (整数
(整数![]() ),对于所有可能的染法,求S的最小值.
),对于所有可能的染法,求S的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已如椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
,![]() 为
为![]() 上的动点.
上的动点.
(1)若![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,试用解析式将
,试用解析式将![]() 表示成
表示成![]() 的函数;
的函数;
(2)试根据![]() 的不同取值,讨论满足
的不同取值,讨论满足![]() 为等腰锐角三角形的点
为等腰锐角三角形的点![]() 的个数.
的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,仅在北京地区每天就有500万单快递等待派送,近5万多名快递员奔跑在一线,快递网点人员流动性也较强,各快递公司需要经常招聘快递员,保证业务的正常开展.下面是50天内甲、乙两家快递公司的快递员每天送货单数统计表:
送货单数 | 30 | 40 | 50 | 60 | |
天数 | 甲 | 10 | 10 | 20 | 10 |
乙 | 6 | 14 | 24 | 6 | |
已知这两家快递公司的快递员日工资方案分别为:甲公司规定底薪![]() 元,每单抽成
元,每单抽成![]() 元;乙公司规定底薪
元;乙公司规定底薪![]() 元,每日前
元,每日前![]() 单无抽成,超过
单无抽成,超过![]() 单的部分每单抽成
单的部分每单抽成![]() 元.
元.
(1)分别求甲、乙快递公司的快递员的日工资![]() (单位:元)与送货单数
(单位:元)与送货单数![]() 的函数关系式;
的函数关系式;
(2)小赵拟到甲、乙两家快递公司中的一家应聘快递员的工作,如果仅从日收入的角度考虑,以这50天的送货单数为样本,将频率视为概率,请你利用所学的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以椭圆的2个焦点与1个短轴端点为顶点的三角形的面积为2
,以椭圆的2个焦点与1个短轴端点为顶点的三角形的面积为2![]() 。
。
(1)求椭圆的方程;
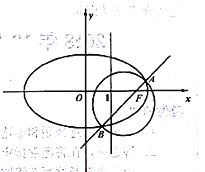
(2)如图,斜率为k的直线l过椭圆的右焦点F,且与椭圆交与A,B两点,以线段AB为直径的圆截直线x=1所得的弦的长度为![]() ,求直线l的方程。
,求直线l的方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com