
【题目】已知向量![]() ,
,![]() ,且函数
,且函数![]() .若函数
.若函数![]() 的图象上两个相邻的对称轴距离为
的图象上两个相邻的对称轴距离为![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)若方程![]() 在
在![]() 时,有两个不同实数根
时,有两个不同实数根![]() ,
,![]() ,求实数
,求实数![]() 的取值范围,并求出
的取值范围,并求出![]() 的值;
的值;
(Ⅲ)若函数![]() 在
在![]() 的最大值为2,求实数
的最大值为2,求实数![]() 的值.
的值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ,
,![]() ;(Ⅲ)
;(Ⅲ)![]() 或
或![]()
【解析】
(Ⅰ)根据三角恒等变换公式化简![]() ,根据周期计算
,根据周期计算![]() ,从而得出
,从而得出![]() 的解析式;(Ⅱ)求出
的解析式;(Ⅱ)求出![]() 在
在![]() ,
,![]() 上的单调性,计算最值和区间端点函数值,从而得出
上的单调性,计算最值和区间端点函数值,从而得出![]() 的范围,根据对称性得出
的范围,根据对称性得出![]() 的值;(Ⅲ)令
的值;(Ⅲ)令![]() ,求出
,求出![]() 的范围和
的范围和![]() 关于
关于![]() 的二次函数,讨论二次函数单调性,根据最大值列方程求出
的二次函数,讨论二次函数单调性,根据最大值列方程求出![]() 的值.
的值.
(Ⅰ)∵![]() ,
,![]() ,
,
∴![]()
![]()
若函数![]() 的图象上两个相邻的对称轴距离为
的图象上两个相邻的对称轴距离为![]() ,
,
则函数![]() 的周期
的周期![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]()
(Ⅱ)由(Ⅰ)知,![]() ,
,
当![]() 时,
时,![]()
∴若方程![]() 在
在![]() 有两个不同实数根,则
有两个不同实数根,则![]() .
.
∴令![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
∴函数在![]() 内的对称轴为
内的对称轴为![]() ,
,
∵![]() ,
,![]() 是方程
是方程![]() ,
,![]() 的两个不同根,
的两个不同根,
∴![]()
(Ⅲ)因为![]() ,所以
,所以![]() ,
,
令![]() ,则
,则![]() .∴
.∴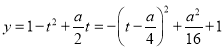
又∵![]() ,由
,由![]() 得
得![]() ,
,
∴![]() .
.
(1)当![]() ,即
,即![]() 时,可知
时,可知![]() 在
在![]() 上为减函数,
上为减函数,
则当![]() 时
时![]() ,
,
由![]() ,解得:
,解得:![]() ,不合题意,舍去.
,不合题意,舍去.
(2)当![]() ,即
,即![]() 时,结合图象可知,当
时,结合图象可知,当![]() 时,
时,![]() ,
,
由![]() ,解得
,解得![]() ,满足题意.
,满足题意.
(3)当![]() ,即
,即![]() 时,知
时,知![]() 在
在![]() 上为增函数,
上为增函数,
则![]() 时,
时,![]() ,由
,由![]() 得
得![]() ,舍去
,舍去
综上,![]() 或
或![]() 为所求.
为所求.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司咪推广线下分店,计划在![]() 市的
市的![]() 区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记
区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记![]() 表示在各区开设分店的个数,
表示在各区开设分店的个数, ![]() 表示这个
表示这个![]() 个分店的年收入之和.
个分店的年收入之和.
| 2 | 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 | 6 |
(1)该公司已经过初步判断,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)假设该公司在![]() 区获得的总年利润
区获得的总年利润![]() (单位:百万元)与
(单位:百万元)与![]() 之间的关系为
之间的关系为![]() ,请结合(1)中的线性回归方程,估算该公司应在
,请结合(1)中的线性回归方程,估算该公司应在![]() 区开设多少个分时,才能使
区开设多少个分时,才能使![]() 区平均每个分店的年利润最大?
区平均每个分店的年利润最大?
(参考公式: ![]() ,其中
,其中 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答
(1)设函数f(x)=|x﹣ ![]() |+|x﹣a|,x∈R,若关于x的不等式f(x)≥a在R上恒成立,求实数a的最大值;
|+|x﹣a|,x∈R,若关于x的不等式f(x)≥a在R上恒成立,求实数a的最大值;
(2)已知正数x,y,z满足x+2y+3z=1,求 ![]() +
+ ![]() +
+ ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
平面直角坐标系xOy中,曲线C:![]() .直线l经过点P(m,0),且倾斜角为
.直线l经过点P(m,0),且倾斜角为![]() .O为极点,以x轴正半轴为极轴,建立极坐标系.
.O为极点,以x轴正半轴为极轴,建立极坐标系.
(Ⅰ)写出曲线C的极坐标方程与直线l的参数方程;
(Ⅱ)若直线l与曲线C相交于A,B两点,且|PA|·|PB|=1,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 中
中![]() ,
,![]() 为
为![]() 的中点.
的中点.
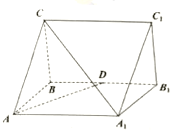
(1)求证:![]() ;
;
(2)若点![]() 为四边形
为四边形![]() 内部及其边界上的点,且三棱锥
内部及其边界上的点,且三棱锥![]() 的体积为三棱柱
的体积为三棱柱![]() 体积的
体积的![]() ,试在图中画出
,试在图中画出![]() 点的轨迹,并说明理由.
点的轨迹,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com