解:(I)由题意f(x)的定义域为(0,+∞),且f'(x)=
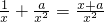
…(2分)
∵a>0,
∴f'(x)>0,
故f(x)在(0,+∞)上是单调递增函数 …(4分)
(II)由(I)可知,f′(x)=
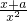
.
(1)若a≥-1,则x+a≥0,即f′(x)≥0在[1,e]上恒成立,此时f(x)在[1,e]上为增函数,
∴[f(x)]
min=f(1)=-a=

,
∴a=-

(舍去) …(5分)
(2)若a≤-e,则x+a≤0,即f′(x)≤0在[1,e]上恒成立,此时f(x)在[1,e]上为减函数,
∴[f(x)]
min=f(e)=1-
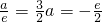
(舍去)…(6分)
(3)若-e<a<-1,令f'(x)=0得x=-a,当1<x<-a时,f'(x)<0,
∴f(x)在(1,-a)上为减函数,f(x)在(-a,e)上为增函数,
∴[f(x)]
min=f(-a)=ln(-a)+1=
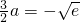
∴[f(x)]
min=f(-a)=ln(-a)+1=

∴a=-

.…(8分)
综上所述,a=-

.
(III)∵f(x)<x
2
∴lnx-

又x>0,∴a>xlnx-x
3…(9分)
令g(x)=xlnx-x
3,h(x)=g′(x)=1+lnx-3x
2,
∴h'(x)=
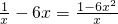
∵x∈(1,+∞)时,h'(x)<0,
∴h(x)在(1,+∞)上是减函数,…(10分)
∴h(x)<h(1)=-2<0
即g'(x)<0∴g(x)在(1,+∞)上也是减函数,
∴g(x)在(1,+∞)上是减函数
∴g(x)<g(1)=-1
∴当a≥-1时,f(x)<x
2在(1,+∞)上恒成立.…(12分)
∴a≥-1
分析:(I)先确定函数f(x)的定义域,再求导函数,从而可判定f(x)在定义域内的单调性;
(II)由(I)可知,f′(x)=
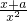
.再分类讨论:a≥-1,f(x)在[1,e]上为增函数;a≤-e,f(x)在[1,e]上为减函数;e<a<-1,f(x)在(1,-a)上为减函数,f(x)在(-a,e)上为增函数,利用f(x)在[1,e]上的最小值为

,可求a的值;
(III)先将不等式整理,再分离参数,构建新函数,利用单调性求出函数值的范围,即可求出a的取值范围.
点评:本题重点考查函数的单调性,考查函数的最值,考查恒成立问题,解题的关键是运用导数,确定函数的单调性,运用分离参数法求解恒成立问题.

 ;
; ,求a的值;
,求a的值;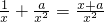 …(2分)
…(2分)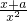 .
. ,
, (舍去) …(5分)
(舍去) …(5分)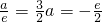 (舍去)…(6分)
(舍去)…(6分)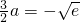

 .…(8分)
.…(8分) .
.
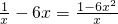 ∵x∈(1,+∞)时,h'(x)<0,
∵x∈(1,+∞)时,h'(x)<0,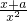 .再分类讨论:a≥-1,f(x)在[1,e]上为增函数;a≤-e,f(x)在[1,e]上为减函数;e<a<-1,f(x)在(1,-a)上为减函数,f(x)在(-a,e)上为增函数,利用f(x)在[1,e]上的最小值为
.再分类讨论:a≥-1,f(x)在[1,e]上为增函数;a≤-e,f(x)在[1,e]上为减函数;e<a<-1,f(x)在(1,-a)上为减函数,f(x)在(-a,e)上为增函数,利用f(x)在[1,e]上的最小值为 ,可求a的值;
,可求a的值;
