
【题目】椭圆![]() 的焦点是
的焦点是![]() ,
,![]() ,且过点
,且过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() 为坐标原点.问椭圆
为坐标原点.问椭圆![]() 上是否存在点
上是否存在点![]() ,使线段
,使线段![]() 和线段
和线段![]() 相互平分?若存在,求出点
相互平分?若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:
【题目】关于函数的对称性有如下结论:对于给定的函数![]() ,如果对于任意的
,如果对于任意的![]() 都有
都有![]() 成立
成立![]() 为常数),则函数
为常数),则函数![]() 关于点
关于点![]() 对称.
对称.
(1)用题设中的结论证明:函数![]() 关于点
关于点![]() ;
;
(2)若函数![]() 既关于点
既关于点![]() 对称,又关于点
对称,又关于点![]() 对称,且当
对称,且当![]() 时,
时,![]() ,求:①
,求:①![]() 的值;
的值;
②当![]() 时,
时,![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,OA、OB、OC所在直线两两垂直,且
中,OA、OB、OC所在直线两两垂直,且![]() ,CA与平面AOB所成角为
,CA与平面AOB所成角为![]() ,D是AB中点,三棱锥
,D是AB中点,三棱锥![]() 的体积是
的体积是![]() .
.
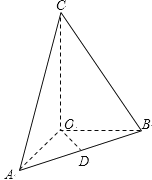
(1)求三棱锥![]() 的高;
的高;
(2)在线段CA上取一点E,当E在什么位置时,异面直线BE与OD所成的角为![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为![]() 的等边三角形
的等边三角形![]() 中,点
中,点![]() 分别是边
分别是边![]() 上的点,满足
上的点,满足![]() 且
且![]()
![]() ,将
,将![]() 沿直线
沿直线![]() 折到
折到![]() 的位置. 在翻折过程中,下列结论成立的是( )
的位置. 在翻折过程中,下列结论成立的是( )
A.在边![]() 上存在点
上存在点![]() ,使得在翻折过程中,满足
,使得在翻折过程中,满足![]() 平面
平面![]()
B.存在![]() ,使得在翻折过程中的某个位置,满足平面
,使得在翻折过程中的某个位置,满足平面![]() 平面
平面![]()
C.若![]() ,当二面角
,当二面角![]() 为直二面角时,
为直二面角时,![]()
D.在翻折过程中,四棱锥![]() 体积的最大值记为
体积的最大值记为![]() ,
,![]() 的最大值为
的最大值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系上,有一点列![]() ,设点
,设点![]() 的坐标
的坐标![]() (
(![]() ),其中
),其中![]() . 记
. 记![]() ,
,![]() ,且满足
,且满足![]() (
(![]() ).
).
(1)已知点![]() ,点
,点![]() 满足
满足![]() ,求
,求![]() 的坐标;
的坐标;
(2)已知点![]() ,
,![]() (
(![]() ),且
),且![]() (
(![]() )是递增数列,点
)是递增数列,点![]() 在直线
在直线![]() :
:![]() 上,求
上,求![]() ;
;
(3)若点![]() 的坐标为
的坐标为![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,点A为该椭圆的左顶点,过右焦点
,点A为该椭圆的左顶点,过右焦点![]() 的直线l与椭圆交于B,C两点,当
的直线l与椭圆交于B,C两点,当![]() 轴时,三角形ABC的面积为18.
轴时,三角形ABC的面积为18.
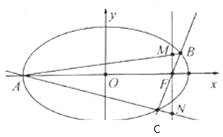
![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]() 如图,当动直线BC斜率存在且不为0时,直线
如图,当动直线BC斜率存在且不为0时,直线![]() 分别交直线AB,AC于点M、N,问x轴上是否存在点P,使得
分别交直线AB,AC于点M、N,问x轴上是否存在点P,使得![]() ,若存在求出点P的坐标;若不存在说明理由.
,若存在求出点P的坐标;若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程
的参数方程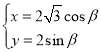 (
(![]() 为参数).直线
为参数).直线![]() 的参数方程
的参数方程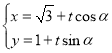 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 在直角坐标系中的普通方程;
在直角坐标系中的普通方程;
(Ⅱ)以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,当曲线
轴的正半轴为极轴建立极坐标系,当曲线![]() 截直线
截直线![]() 所得线段的中点极坐标为
所得线段的中点极坐标为![]() 时,求直线
时,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com