
【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少?”,共有4个选项:A,1.5小时以上,B,1-1.5小时,C,0.5-1小时,D,0.5小时以下.图(1),(2)是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
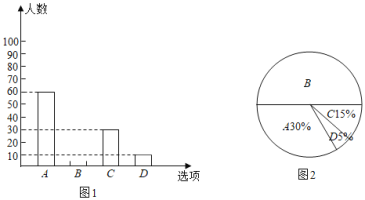
(1)本次一共调查了多少名学生.
(2)在图(1)中将![]() 对应的部分补充完整.
对应的部分补充完整.
(3)若该校有3000名学生,你估计全校有多少名学生平均每天参加体育活动的时间在0.5小时以下?
科目:高中数学 来源: 题型:
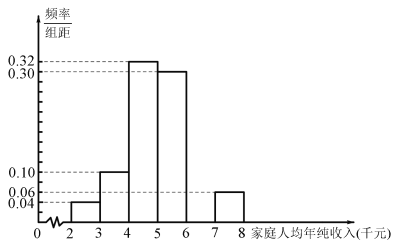
【题目】某贫困地区截至2018年底,按照农村家庭人均年纯收入8000元的小康标准,该地区仅剩部分家庭尚未实现小康.现从这些尚未实现小康的家庭中随机抽取50户,得到这50户家庭2018年的家庭人均年纯收入的频率分布直方图.
(1)补全频率分布直方图,并求出这50户家庭人均年纯收入的中位数和平均数(精确到元);
(2)2019年7月,为估计该地能否在2020年全面实现小康,统计了该地当时最贫困的一个家庭2019年1至6月的人均月纯收入如表:
月份/2019(时间代码 | 1 | 2 | 3 | 4 | 5 | 6 |
人居月纯收入 (元) | 275 | 365 | 415 | 450 | 470 | 485 |
由散点图及相关性分析发现:家庭人均月纯收入![]() 与时间代码
与时间代码![]() 之间具有较强的线性相关关系,请求出回归直线方程;并由此估计该家庭2020年1月的家庭人均月纯收入.
之间具有较强的线性相关关系,请求出回归直线方程;并由此估计该家庭2020年1月的家庭人均月纯收入.
①可能用到的数据:![]() ;
;
②参考公式:线性回归方程![]() 中,
中,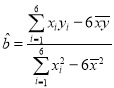 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知AB是圆O的直径,C是圆O上一点,AC=BC,且PA⊥平面ABC,E是AC的中点,F是PB的中点,PA=![]() ,AB=2.求:
,AB=2.求:
(Ⅰ)异面直线EF与BC所成的角;
(Ⅱ)点A到平面PBC的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用0,1,2,3,4这五个数字组成无重复数字的自然数.
(Ⅰ)在组成的三位数中,求所有偶数的个数;
(Ⅱ)在组成的三位数中,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如301,423等都是“凹数”,试求“凹数”的个数;
(Ⅲ)在组成的五位数中,求恰有一个偶数数字夹在两个奇数数字之间的自然数的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中装有除颜色外其他均相同的编号为a,b的两个黑球和编号为c,d,e的三个红球,从中任意摸出两个球.
(1)求恰好摸出1个黑球和1个红球的概率:
(2)求至少摸出1个黑球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,且椭圆四个顶点构成的菱形面积为
,且椭圆四个顶点构成的菱形面积为![]() .
.
(1)求椭圆C的方程;
(2)若直线l :y=x+m与椭圆C交于M,N两点,以MN为底边作等腰三角形,顶点为P(3,-2),求m的值及△PMN的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com