
【题目】已知函数![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() )的图象与
)的图象与![]() 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为![]() ,且图象上一个最低点为
,且图象上一个最低点为![]() .
.
(1)求![]() 的解析式,对称轴及对称中心.
的解析式,对称轴及对称中心.
(2)该图象可以由![]() 的图象经过怎样的变化得到.
的图象经过怎样的变化得到.
(3)当![]() ,求
,求![]() 的值域.
的值域.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据函数![]() 的图象与性质,现确定周期得出
的图象与性质,现确定周期得出![]() 的值,再确定振幅得到A的值,最后代入点的坐标,求解
的值,再确定振幅得到A的值,最后代入点的坐标,求解![]() 的值,即可得到函数的解析式;
的值,即可得到函数的解析式;
(2)根据三角函数图象的平移变换和伸缩变换,即可得到求解;
(3)由![]() ,求得
,求得![]() ,得到函数
,得到函数![]() 的最大值与最小值,即可得到函数的值域.
的最大值与最小值,即可得到函数的值域.
解:(1)由题意,图象与![]() 轴相邻两个交点直接距离为
轴相邻两个交点直接距离为![]() ,
,
可得![]() ,∴
,∴![]() ,
,
又∵图象上一个最低点为![]() ,且
,且![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
因此,![]() .
.
对称轴:∵![]() ,
,![]() ,
,
∴对称轴方程为![]() ,
,![]() .
.
对称中心:∵![]() ,
,![]()
∴函数的对称中心为![]() ,
,![]() .
.
(2)将![]() 的图象向左平移
的图象向左平移![]() ,得到
,得到![]() ,再将横坐标缩小原来的
,再将横坐标缩小原来的![]() ,
,
纵坐标不变得到![]() ,再横坐标不变,纵坐标伸长为原来的
,再横坐标不变,纵坐标伸长为原来的![]() 倍得到
倍得到![]() .
.
(3)当![]() ,则
,则![]() ,
,
∴当![]() 时,即
时,即![]() ,
,![]() ,
,
当![]() 时,即
时,即![]() ,
,![]() ,
,
故得![]() 的值域是
的值域是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,平面![]() 与平面
与平面![]() 交于直线
交于直线![]() 是平面
是平面![]() 内不同的两点,
内不同的两点,![]() 是平面
是平面![]() 内不同的两点,且
内不同的两点,且![]() 不在直线
不在直线![]() 上,
上,![]() 分别是线段
分别是线段![]() 的中点,下列命题中正确的个数为( )
的中点,下列命题中正确的个数为( )
①若![]() 与
与![]() 相交,且直线
相交,且直线![]() 平行于
平行于![]() 时,则直线
时,则直线![]() 与
与![]() 也平行;
也平行;
②若![]() 是异面直线时,则直线
是异面直线时,则直线![]() 可能与
可能与![]() 平行;
平行;
③若![]() 是异面直线时,则不存在异于
是异面直线时,则不存在异于![]() 的直线同时与直线
的直线同时与直线![]() 都相交;
都相交;
④![]() 两点可能重合,但此时直线
两点可能重合,但此时直线![]() 与
与![]() 不可能相交
不可能相交

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,-2),椭圆E: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为![]() ,O为坐标原点.
,O为坐标原点.
(1)求E的方程;
(2)设过点A的动直线l与E相交于P,Q两点.当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,平面AED⊥平面ABNCD,EF∥AB,AB=2,BC=EF=1,AE= ![]() ,∠BAD=60°,G为BC的中点.
,∠BAD=60°,G为BC的中点. 
(1)求证:FG∥平面BED;
(2)求证:平面BED⊥平面AED;
(3)求直线EF与平面BED所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=![]() ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点.
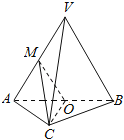
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB
(3)求三棱锥V﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列几个命题
①方程![]() 有一个正实根,一个负实根,则
有一个正实根,一个负实根,则![]() ;
;
②函数![]() 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
③命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”;
”;
④命题“![]() ,使得
,使得![]() ”的否定是“
”的否定是“![]() ,都有
,都有![]() ”;
”;
⑤“![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差d≠0,且a3 , a5 , a15成等比数列,若a1=3,Sn为数列an的前n项和,则anSn的最小值为( )
A.0
B.﹣3
C.﹣20
D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com