
(1)设三条网线可通过的最大信息总量为x,已知当x≥7时,可保证线路信息畅通,求线路信息畅通的概率;
(2)为保证网络在x≥7时信息畅通的概率超过0.85,需要增加一条最大信息量为n(n≥3)的网线与原有4条线路并联,问满足条件的n的最小值是多少?

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
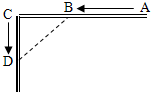 汽车和自行车分别从A地和C地同时开出,如图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米.(汽车开到C地即停止)
汽车和自行车分别从A地和C地同时开出,如图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米.(汽车开到C地即停止)查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省温州市龙湾中学高一(上)第一次月考数学试卷(解析版) 题型:解答题
 汽车和自行车分别从A地和C地同时开出,如图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米.(汽车开到C地即停止)
汽车和自行车分别从A地和C地同时开出,如图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米.(汽车开到C地即停止)查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省扬州市邗江中学高一(上)期中数学试卷(解析版) 题型:解答题
 汽车和自行车分别从A地和C地同时开出,如图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米.(汽车开到C地即停止)
汽车和自行车分别从A地和C地同时开出,如图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米.(汽车开到C地即停止)查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省温州市龙湾中学高一(上)第一次月考数学试卷(解析版) 题型:解答题
 汽车和自行车分别从A地和C地同时开出,如图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米.(汽车开到C地即停止)
汽车和自行车分别从A地和C地同时开出,如图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米.(汽车开到C地即停止)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com