Question

【题目】在四棱锥中，平面，，，，点在线段上，且，为线段的中点.

（1）求证：平面；

（2）若，求三棱锥的体积.

Answer 1

【答案】（1）见解析（2）

【解析】

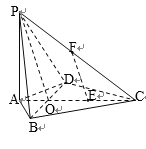
（1）设AC∩BD＝O，连接PO，通过证明EF为△POC的中位线，推出EF∥PO，然后EF∥平面PBD．

（2）利用VF﹣PADVC﹣PADVP﹣CAD，求解几何体的体积即可．

(1) ∵AB＝AD，CB＝CD,∴AC⊥BD,设AC∩BD＝O,连接PO，

由AB＝AD＝2，∠BAD=120

得：OA＝1，BD＝2,在RtCOD中，CD＝， OD＝

∴OC＝2

∵AE＝2EC，

∴E为OC中点

又∵F为PC的中点

∴EF为POC的中位线

∴EF∥PO

又PO面PBD EF面PBD

∴EF∥平面PBD

（2）在Rt△PAC中，PC＝5，由（1）可知AC＝3，∴PA＝4

∴VF-PAD=VC-PAD=VP-CAD=×VP-ABCD=×××3×2×4=