
【题目】如图,正四棱锥![]() 中底面边长为
中底面边长为![]() ,侧棱
,侧棱![]() 与底面
与底面![]() 所成角的正切值为
所成角的正切值为![]() .
.
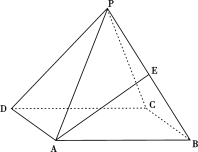
(1)求正四棱锥![]() 的外接球半径;
的外接球半径;
(2)若E是PB中点,求异面直线PD与AE所成角的正切值.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)求外切球的半径首先确定圆心的位置,进而得到求得半径;(2)容易证明EO∥PD且EO=![]() PD可得∠AEO就是异面直线PD与AE所成的角,在Rt△AOE中求
PD可得∠AEO就是异面直线PD与AE所成的角,在Rt△AOE中求
试题解析:(1)连结AC,BD交于点O,连结PO,则PO⊥面ABCD,
∴ ∠PAO就是PA与底面ABCD所成的角,∴ tan∠PAO=![]() .
.
又AB=![]() ,则PO=AOtan∠PAO =
,则PO=AOtan∠PAO =![]() .
.
设F为外接球球心,连FA,
易知FA=FP,设FO=x,则
![]()
![]()
(2)连结EO,由于O为BD中点,E为PD中点,所以![]()
![]()
![]() .
.
∴ ![]() 就是异面直线PD与AE所成的角.
就是异面直线PD与AE所成的角.
在Rt![]() 中,
中,![]() .∴
.∴![]() .
.
由![]() ,
,![]() 可知
可知![]() 面
面![]() .所以
.所以![]() ,
,
在Rt![]() 中,
中,![]() ,
,
即异面直线PD与AE所成角的正切值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,并且
,并且![]() ,数列
,数列![]() 满足:
满足:![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() 及前
及前![]() 项和为
项和为![]() ;
;
(2)求数列![]() 的通项公式
的通项公式![]() 及前
及前![]() 项和为
项和为![]() ;
;
(3)记集合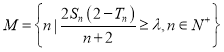 ,若
,若![]() 的子集个数为16,求实数
的子集个数为16,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为集合A,已知集合B={x|1<x<3},C={x|x≥m},全集为R.
的定义域为集合A,已知集合B={x|1<x<3},C={x|x≥m},全集为R.
(1)求(RA)∩B;
(2)若(A∪B)∩C≠,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①垂直于同一平面的两条直线相互平行;
②平行于同一平面的两条直线相互平行;
③若一条直线平行于一个平面内的无数条直线,那么这条直线平行于这个平面;
④若一条直线垂直于一个平面内的任一条直线,那么这条直线垂直于这个平面.
其中真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据统计资料,我国能源生产自1992年以来发展很快,下面是我国能源生产总量(折合亿吨标准煤)的几个统计数据:1992年8.6亿吨,5年后的1997年10.4亿吨,10年后的2002年12.9亿吨.有关专家预测,到2007年我国能源生产总量将达到17.1亿吨,则专家是依据下列哪一类函数作为数学模型进行预测的( )
A.一次函数 B.二次函数 C.指数函数 D.对数函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:函数f(x)=loga(2+x)-loga(2-x)(a>0且a≠1)
(Ⅰ)求f(x)定义域;
(Ⅱ)判断f(x)的奇偶性,并说明理由;
(Ⅲ)求使f(x)>0的x的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将参加夏令营的500名学生编号为:001,002,…,500,采用系统抽样的方法抽取一个容量为50的样本,且随机抽得的号码为003,这500名学生分住在三个营区,从001到200在第一营区,从201到355在第二营区,从356到500在第三营区,三个营区被抽中的人数分别为( )
A.20,15,15 B.20,16,14 C.12,14,16 D.21,15,14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com