
【题目】已知数列{an}满足a1=2,前n项和为Sn , 若Sn=2(an﹣1),(n∈N+).
(1)求数列{an}的通项公式;
(2)设bn=(log2an+1)2﹣(log2an)2 , 若cn=anbn , 求{cn}的前n项和Tn .
【答案】
(1)解:∵Sn=2(an﹣1),
∴当n≥2时,an=Sn﹣Sn﹣1=2(an﹣1)﹣2(an﹣1﹣1)
=2(an﹣an﹣1),则an=2an﹣1,
又a1=2,则数列{an}是以2为首项、公比的等比数列,
∴ ![]() =2n
=2n
(2)解:由(1)得,bn=(log2an+1)2﹣(log2an)2
=(n+1)2﹣n2=2n+1,
∴cn=anbn=(2n+1)2n,
∴Tn=3×2+5×22+…+(2n+1)×2n,①
则2Tn=3×22+5×23+…+(2n+1)×2n+1,②
①﹣②得:﹣Tn=6+2(22+23+…+2n)﹣(2n+1)2n+1
=6+2× ![]() ﹣(2n+1)2n+1=(﹣2n+1)2n+1﹣2,
﹣(2n+1)2n+1=(﹣2n+1)2n+1﹣2,
∴Tn=(2n﹣1)2n+1+2
【解析】(1)由题意和当n≥2时an=Sn﹣Sn﹣1进行化简,得到数列的递推公式,由等比数列的定义判断出数列{an}是等比数列,由等比数列的通项公式求出{an}的通项公式;(2)由(1)和对数的运算化简bn=(log2an+1)2﹣(log2an)2 , 代入cn=anbn化简后,利用错位相减法和等比数列的前n项和公式求Tn .
【考点精析】关于本题考查的数列的前n项和和数列的通项公式,需要了解数列{an}的前n项和sn与通项an的关系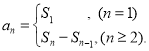 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】定义在(﹣∞,0)∪(0,+∞)上的函数f(x),总有f(mn)=f(m)f(n),且f(x)>0,当x>1时,f(x)>1.
(1)求f(1),f(﹣1)的值;
(2)判断函数的奇偶性,并证明;
(3)判断函数在(0,+∞)上的单调性,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体中,四边形![]() 为菱形,对角线
为菱形,对角线![]() 与
与![]() 的交点为
的交点为![]() ,四边形
,四边形![]() 为梯形,
为梯形, ![]() .
.

(Ⅰ)若![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,
, ![]() ,
, ![]() ,求
,求![]() 与平面
与平面![]() 所成角.
所成角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且满足2acosC﹣(2b﹣c)=0.
(1)求角A;
(2)若sinC=2sinB,且a= ![]() ,求边b,c.
,求边b,c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=asin 2x+bcos 2x,其中a,b∈R,ab≠0.若f(x)≤|f( ![]() )|对一切x∈R恒成立,则以下结论正确的是(写出所有正确结论的编号). ①
)|对一切x∈R恒成立,则以下结论正确的是(写出所有正确结论的编号). ① ![]() ;②
;② ![]() ≥
≥ ![]() ;
;
③f(x)的单调递增区间是(kπ+ ![]() ,kπ+
,kπ+ ![]() )(k∈Z);
)(k∈Z);
④f(x)既不是奇函数也不是偶函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学高三年级甲乙两班各10名同学,测量出他们的身高(单位:cm),获得身高数据的茎叶图如图.其中甲班有一个数据被污损.
(Ⅰ)若已知甲班同学身高平均数为170cm,求污损处的数据;
(Ⅱ)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x2﹣3x+1, ![]() ,(A≠0)
,(A≠0)
(1)当0≤x≤ ![]() 时,求y=f(sinx)的最大值;
时,求y=f(sinx)的最大值;
(2)若对任意的x1∈[0,3],总存在x2∈[0,3],使f(x1)=g(x2)成立,求实数A的取值范围;
(3)问a取何值时,方程f(sinx)=a﹣sinx在[0,2π)上有两解?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com