
����Ŀ��ij��λ��������һ������������Ϊ������״������2.5�ף���ǰ��ǽ��2.5�ߵIJ�ɫ�ְ壬������2.5�ߵĸ��ϸְ壬���ְָ�ļ۸��ó��������㣨�����ְ�ĸ߾�Ϊ2.5�ף��øְ�ij��ȳ��Ե��۾������ְ�ļ۸�ÿ���ۣ���ɫ�ְ�Ϊ450Ԫ�����ϸְ�Ϊ200Ԫ���������������Ͻ��죬ÿƽ���ײ��Ϸ�Ϊ200Ԫ��ÿ�����Ϸѿ�����32000Ԫ���ڣ�
��1���跿ǰ��ǽ�ij�Ϊx������ǽ�ij�Ϊy�����ò��Ϸ�Ϊp������x��y��ʾp��
��2���ڲ��ϷѵĿ����¼������S�����ֵ�Ƕ��٣���ָ��ǰ��ǽ�ij���xӦΪ������ʱS���
���𰸡�
��1���⣺����ã�p=2x��450+2y��200+xy��200=900x+400y+200xy
��p=900x+400y+200xy
��2���⣺��S=xy����p=900x+400y+200xy�� ![]() +200S=200S+1200
+200S=200S+1200 ![]() ��
��
����Ϊp��3200������200S+1200 ![]() ��3200��
��3200��
��é�16�� ![]() ��10��
��10��
��S��0����0��S��100�����ҽ��� ![]() ����x=
����x= ![]() ʱSȡ�����ֵ
ʱSȡ�����ֵ
����������1����������ɷֱ����ǰ��ǽ������ǽ�ͷ����ķ��ã�������Ӽ������P����2������P�ı���ʽ�ͻ�������ʽ��ù��� ![]() �IJ���ʽ��ϵ�����
�IJ���ʽ��ϵ����� ![]() �ķ�Χ���Լ��Ⱥų����������x��ֵ��
�ķ�Χ���Լ��Ⱥų����������x��ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У�������ȷ������У� ��
����ͬһ����ϵ�У�����y=2x�뺯��y=log2x��ͼ�����ֱ��y=x�Գƣ�
�ں���f��x��=ax+1��a��0����a��1����ͼ�����㣨0��2����
�ۺ��� ![]() �����ֵΪ1��
�����ֵΪ1��
����ȡx��R������3x��2x ��
A.�٢ڢۢ�
B.��
C.�٢�
D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() =1��a��b��0����һ������ΪA��2��0����������Ϊ
=1��a��b��0����һ������ΪA��2��0����������Ϊ ![]() ��ֱ��y=k��x��1������ԲC���ڲ�ͬ������ M��N��
��ֱ��y=k��x��1������ԲC���ڲ�ͬ������ M��N��
��1������ԲC�ķ��̣������佹�����ꣻ
��2������AMN�����Ϊ ![]() ʱ����k��ֵ��
ʱ����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����������ABCD��A��B��C��D���У�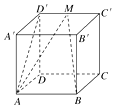
��1��������D�䣭AB��D�Ĵ�С��
��2����M��C��D����е㣬������M��AB��D�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���β���ʽax2+2x+b��0�Ľ⼯Ϊ{x|x��c}���� ![]() ������a+c��0����ȡֵ��ΧΪ ��
������a+c��0����ȡֵ��ΧΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x���Ƕ�����R������2Ϊ���ڵ�ż��������0��x��1��f��x��=x2 �� �������g��x��=f��x������x+m����������㣬��ʵ��m��ֵΪ�� ��
A.2k��k��Z��
B.2k��2k+ ![]() ��k��Z��
��k��Z��
C.0
D.2k��2k�� ![]() ��k��Z��
��k��Z��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ����ֱ�� x 2 y 3 = 0 �ϣ��ҹ���A(2��-3),B(-2��-5)��ԲC�ķ���.
��1����Բ����ֱ�� ![]() �ϣ��ҹ���A(2��-3),B(-2��-5)��ԲC�ķ���.
�ϣ��ҹ���A(2��-3),B(-2��-5)��ԲC�ķ���.
��2���� ![]() ��ԲC�ϵĵ㣬��
��ԲC�ϵĵ㣬�� ![]() �����ֵ����Сֵ.
�����ֵ����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ ![]() ��
�� ![]() ����ƽ�滥�ഹֱ����
����ƽ�滥�ഹֱ���� ![]() �ֱ���
�ֱ��� ![]() ��
�� ![]() ���е㣬��ô
���е㣬��ô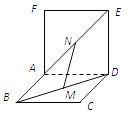
�� ![]() �� ��
�� �� ![]() ƽ��
ƽ�� ![]() ����
���� ![]() ����
���� ![]() ���棬���м�����ĸ���Ϊ�� ��
���棬���м�����ĸ���Ϊ�� ��
A.4
B.3
C.2
D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��H��x0 �� y0����ԲC��x2+y2+Dx+Ey+F=0�����е�CΪԲ�ģ�D2+E2��4F��0���⣬�ɵ�H��ԲC�����ߣ�����һ���е�ΪM��
��֤��|HM|= ![]() ��
��
��1����֪��H��x0 �� y0����ԲC��x2+y2+Dx+Ey+F=0�����е�CΪԲ�ģ�D2+E2��4F��0���⣬�ɵ�H��ԲC�����ߣ�����һ���е�ΪM��
��֤��|HM|= ![]() ��
��
��2����ͼ��P��ֱ��x=4��һ���㣬��PΪԲ�ĵ�ԲP������B��1��0����ֱ��l��ԲP�ڵ�B�������ߣ���A����1��0����ԲP���������߷ֱ���l����E��F���㣮
��֤��|EA|+|EB|Ϊ��ֵ��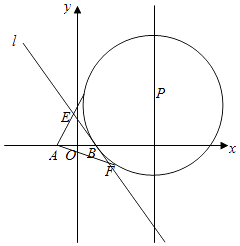
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com