练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】给出下列几个命题：①三点确定一个平面；②一个点和一条直线确定一个平面；③垂直于同一直线的两直线平行；④平行于同一直线的两直线平行.其中正确命题的序号是____.

    【答案】④

    【解析】分析：由三点可能共线可判断①错；由点可能在直线上可判断②错；由两直线可能相交、异面判断③错；根据公理可判定④正确.

    详解：①不共线的三点确定一个平面，故①错误；

    ②一条直线和直线外一点确定一个平面，故②错误；

    ③垂直于同一直线的两直线相交、平行或异面，故③错误；

    ④平行于同一直线的两直线平行，故④正确，故答案为④.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图（1）所示，在直角梯形ABCP中，BC∥AP，AB⊥BC，CD⊥AP，AD＝DC＝PD＝2，E、F、G分别为线段PC、PD、BC的中点，现将△PDC折起，使平面PDC⊥平面ABCD（图（2））．

    （1）求证：AP∥平面EFG；

    （2）若点Q是线段PB的中点，求证：PC⊥平面ADQ；

    （3）求三棱锥C－EFG的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设集合A＝{x|x＞－1}，B＝{x||x|≥1}，则“x∈A且xB”成立的充要条件是(　　)

    A. －1＜x≤1 B. x≤1

    C. x＞－1 D. －1＜x＜1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】班主任想对本班学生的考试成绩进行分析，决定从全班名女同学，名男同学中随机抽取一个容量为的样本进行分析．

    （1）如果按性别比例分层抽样，男、女生各抽取多少位才符合抽样要求？

    （2）随机抽出位，他们的数学、地理成绩对应如下表：

    ①若规定分以上（包括分）为优秀，在该班随机调查一位同学，该同学的数学和地理成绩均为优秀的概率是多少？

    ②根据上表，用变量与的相关系数或用散点图说明地理成绩与数学成绩之间线性相关关系的强弱．如果有较强的线性相关关系，求出与的线性回归方程（系数精确到）；如果不具有线性相关关系，说明理由．

    参考公式：

    相关系数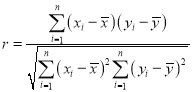；回归直线的方程是：，

    其中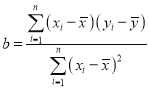，，是与对应的回归估计值．

    参考数据：，，，，

    ，，，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列叙述错误的是(　　)

    A. 若事件A发生的概率为P(A),则0≤P(A)≤1

    B. 互斥事件不一定是对立事件,但是对立事件一定是互斥事件

    C. 两个对立事件的概率之和为1

    D. 对于任意两个事件A和B,都有P(A∪B)=P(A)+P(B)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】7个人站成一排，其中甲一定站在最左边，乙和丙必须相邻，一共有______种不同排法

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知.

    （1）讨论的单调性；

    （2）当时, 证明对于任意的成立.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在用“等值算法”求98和56的最大公约数时,操作如下:(98,56)→(42,56)→(42,14)→(28,14)→(14,14),由此可知两数的最大公约数为(　　)

    A. 98 B. 56 C. 14 D. 42

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等比数列的前项和为，且为等差数列的前三项．

    （1）求与数列的通项公式；

    （2）设数列的前项和，试问是否存在正整数，对任意的使得？若存在请求出的最大值，若不存在请说明理由．

    查看答案和解析>>

    同步练习册答案