
【题目】已知函数f(x)=ax3-![]() x2+1(xR),其中a>0.
x2+1(xR),其中a>0.
(1)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)若在区间![]() 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.
【答案】(1)y=6x-9.(2)0<a<5.
【解析】试题分析:(1)利用导数求切线斜率即可;
(2)在区间![]() 上,
上,![]() 恒成立
恒成立![]() 恒成立,令
恒成立,令![]() ,解得
,解得![]() 或
或![]() ,以下分两种情况
,以下分两种情况![]() ,
,![]() 讨论,分类求出函数最大值即可.
讨论,分类求出函数最大值即可.
试题解析:(1)当a=1时,f(x)=x3-x2+1,f(2)=3;f' (x)=3x2-3x, f' (2)=6.
所以曲线y=f(x) 在点(2,f(2))处的切线方程y-3=6(x-2),即y=6x-9.
(2)f' (x)=3ax2-3x=3x(ax-1),令f' (x)=0,解得x=0或x=.
以下分两种情况讨论:
①若0<a≤2,则≥,当x变化时,f' (x),f(x)的变化情况如下表:
x | (-,0) | 0 | (0,) |
f' (x) | + | 0 | - |
f(x) | 递增 | 极大值 | 递减 |
当x[-,]上,f(x)>0等价于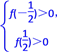 ,即
,即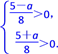 解不等式组得-5<a<5.因此0<a≤2.
解不等式组得-5<a<5.因此0<a≤2.
②若a>2,则0<<,当x变化时,f' (x),f(x)的变化情况如下表:
X | (-,0) | 0 | (0,) | (,) | |
f' (x) | + | 0 | - | 0 | + |
f'(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
当x[-,]上,f(x)>0等价于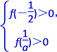 ,即
,即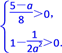 解不等式组得
解不等式组得![]() <a<5,或a<-
<a<5,或a<-![]() .因此2<a<5. 综合①和②,可知a的取值范围为0<a<5.
.因此2<a<5. 综合①和②,可知a的取值范围为0<a<5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某市某水产养殖户进行小龙虾销售,已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价![]() (元/千克)与时间第
(元/千克)与时间第![]() (天)之间的函数关系为:
(天)之间的函数关系为:
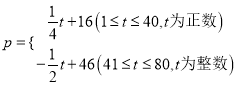 ,日销售量
,日销售量![]() (千克)与时间第
(千克)与时间第![]() (天)之间的函数关系如图所示:
(天)之间的函数关系如图所示:
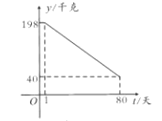
(1)求日销售量![]() 与时间
与时间![]() 的函数关系式?
的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)在实际销售的前40天中,该养殖户决定每销售1千克小龙虾,就捐赠![]() 元给村里的特困户,在这前40天中,每天扣除捐赠后的日销售利润随时间
元给村里的特困户,在这前40天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
, ![]() .设
.设![]() (t为实数).
(t为实数).
(Ⅰ)若![]() ,求当
,求当![]() 取最小值时实数t的值;
取最小值时实数t的值;
(Ⅱ)若![]() ⊥
⊥![]() ,问:是否存在实数t,使得向量
,问:是否存在实数t,使得向量![]() -
-![]() 和向量
和向量![]() 的夹角为
的夹角为![]() ,若存在,请求出t;若不存在,请说明理由.
,若存在,请求出t;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线C:y2=2px(p>0)的准线为l,焦点为F.⊙M的圆心在x轴的正半轴上,且与y轴相切.过原点O作倾斜角为![]() 的直线n交l于点A, 交⊙M于另一点B,且AO=OB=2.
的直线n交l于点A, 交⊙M于另一点B,且AO=OB=2.
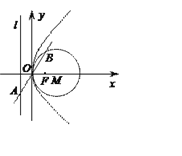
(1)求⊙M和抛物线C的方程;
(2)若P为抛物线C上的动点,求![]() 的最小值;
的最小值;
(3)过l上的动点Q向⊙M作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
已知函数f(x)=|2x+1|+|2x-a|.
(I)若f(x)的最小值为2,求a的值;
(II)若f(x)≤|2x-4|的解集包含[-2,-1],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的一个焦点为![]() ,对应于这个焦点的准线方程为
,对应于这个焦点的准线方程为![]()
(1)写出抛物线C的方程;
(2)过F点的直线与曲线C交于A、B两点,O点为坐标原点,求△AOB重心G的轨迹方程;
(3)点P是抛物线C上的动点,过点P作圆![]() 的切线,切点分别是M,N.当P点在何处时,|MN|的值最小?求出|MN|的最小值.
的切线,切点分别是M,N.当P点在何处时,|MN|的值最小?求出|MN|的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com