
【题目】已知点A(2,0),点B(﹣2,0),直线l:(λ+3)x+(λ﹣1)y﹣4λ=0(其中λ∈R).
(1)求直线l所经过的定点P的坐标;
(2)若直线l与线段AB有公共点,求λ的取值范围;
(3)若分别过A,B且斜率为 ![]() 的两条平行直线截直线l所得线段的长为4
的两条平行直线截直线l所得线段的长为4 ![]() ,求直线l的方程.
,求直线l的方程.
【答案】
(1)解:由题意,(λ+3)x+(λ﹣1)y﹣4λ=0(其中λ∈R),
则λ(x+y﹣4)+(3x﹣y)=0,
∵λ∈R,
∴ ![]() ,
,
解的 ![]() ,
,
∴直线l所经过的定点P的坐标(1,3)
(2)解:∵点A(2,0),点B(﹣2,0),定点P的坐标(1,3);
∴kPA= ![]() =﹣3,kPB=
=﹣3,kPB= ![]() =1,
=1,
∵直线l与线段AB有公共点,
当λ=1时,直线x=1,与线段AB有公共点,
当λ≠1时,直线l的斜率k= ![]() ,
,
∴ ![]() ≥1或
≥1或 ![]() ≤﹣3,
≤﹣3,
解的﹣1≤λ<1,或1<λ≤3,
综上所述:λ的取值范围为[﹣1,3]
(3)解:分别过A,B且斜率为 ![]() 的两条平行直线,分别为y=
的两条平行直线,分别为y= ![]() x+2
x+2 ![]() ,y=
,y= ![]() x﹣2
x﹣2 ![]() ,
,
由(1)知,l恒过点(1,3),
当斜率存在时,设直线l为y﹣3=k(x﹣1),由图象易知,直线l的倾斜角为30°,即k= ![]() ,
,
∴过点p的直线l为y﹣3= ![]() (x﹣1),即
(x﹣1),即 ![]() x﹣3y+9﹣
x﹣3y+9﹣ ![]() =0.
=0.
当直线l的斜率不存在时,由(1)可知直线过定点(1,3),则直线方程为x=1,
令x=1,可知y1=3 ![]() ,y2=﹣
,y2=﹣ ![]() ,|y1﹣y2|=4
,|y1﹣y2|=4 ![]() ,符合题意,
,符合题意,
综上所述:直线l的方程为x=1或 ![]() x﹣3y+9﹣
x﹣3y+9﹣ ![]() =0
=0
【解析】(1)由题意,(λ+3)x+(λ﹣1)y﹣4λ=0(其中λ∈R),由此可得方程组,从而可求定点的坐标;(2)求出A,B与定点的斜率,即可得到λ的取值范围;(3)先求出过A,B且斜率为 ![]() 的两条平行直线,再分直线l的斜率存在和不存在两种情况讨论即可.
的两条平行直线,再分直线l的斜率存在和不存在两种情况讨论即可.
【考点精析】解答此题的关键在于理解一般式方程的相关知识,掌握直线的一般式方程:关于![]() 的二元一次方程
的二元一次方程![]() (A,B不同时为0).
(A,B不同时为0).


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an=3an﹣1+3n﹣1(n∈N*,n≥2)且a3=95.
(1)求a1 , a2的值;
(2)求实数t,使得bn= ![]() (an+t)(n∈N*)且{bn}为等差数列;
(an+t)(n∈N*)且{bn}为等差数列;
(3)在(2)条件下求数列{an}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣log3(9x)log3 ![]() (
( ![]() ≤x≤27).
≤x≤27).
(1)设t=log3x,求t的取值范围
(2)求f(x)的最小值,并指出f(x)取得最小值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程x2+mx+1=0有两个不等的负实数根;命题q:方程4x2+4(m﹣2)x+1=0无实数根.
(1)若“¬p”为假命题,求m范围;
(2)若“p或q”为真命题,“p且q”为假命题,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在下图中的两条线段上,该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示. 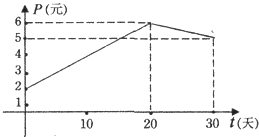
第t天 | 4 | 10 | 16 | 22 |
Q(万股) | 36 | 30 | 24 | 18 |
(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)在(2)的结论下,用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几日交易额最大,最大值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com