
分析 ①平面内无数条直线均为平行线时,不能得出直线与这个平面垂直,故①错误;②垂直于这条直线的直线与这个平面可以是任何的位置关系,故②错误.若a∥α,b⊥α,则根据线面平行、垂直的性质,必有a⊥b.
解答 解:①平面内无数条直线均为平行线时,不能得出直线与这个平面垂直,将“无数条”改为“所有”才正确;故①错误;
②垂直于这条直线的直线与这个平面可以是任何的位置关系,有可能是平行、相交、线在面内,故②错误.
③若a∥α,b⊥α,则根据线面平行、垂直的性质,必有a⊥b,正确;
④若a⊥b,则过b有且只有一个平面与a垂直,显然正确.
故答案为③④.
点评 本题考查空间的线面位置关系,考查空间想象能力和逻辑推理能力.


科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 14 | C. | 3 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
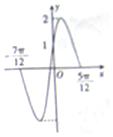
| A. | -1 | B. | 1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{11}$ | B. | $\frac{2}{11}$ | C. | $\frac{11}{2}$ | D. | -$\frac{11}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com