
分析 (1)求出f(x)的导数,配方,可得导数非负,即可判断不存在;
(2)由于f(x)在[a,+∞)上有零点,则f(x)在[a,+∞)上的最小值小于等于0.求出f(x)的导数,极值点,讨论a的范围,解不等式,求并集即可得到所求a的范围.
解答 解:(1)当a=2时,f(x)=ex(x2+2x+2),
导数为f′(x)=ex(x2+4x+4)=ex(x+2)2≥0,
对任意的x1,x2∈R,均有f′(x1)f′(x2)≥0,
故函数y=f(x)的图象上不存在两条相互垂直的切线;
(2)由于f(x)在[a,+∞)上有零点,则f(x)在[a,+∞)上的最小值小于等于0.
由f′(x)=ex(x+2)(x+a),令f′(x)=0,可得x=-2或-a.
当-a≤-2时,即a≥2时,f′(x)>0对x∈[a,+∞)成立,均有f(x)在[a,+∞)递增,
此时f(x)的最小值为f(a)=ea(a2+a2+a)≤ea,
解得-1≤a≤$\frac{1}{2}$,不成立;
当-a>-2即a<2时,
①若a≥0,f′(x)>0对x∈[a,+∞)成立,均有f(x)在[a,+∞)递增,
此时f(x)的最小值为f(a)=ea(a2+a2+a)≤ea,
解得-1≤a≤$\frac{1}{2}$,即为0≤a≤$\frac{1}{2}$;
②若a<0,若a≥-2,f′(x)<0对x∈(a,-a)成立,f′(x)>0对x∈[-a,+∞)成立,
则f(x)在(a,-a)递减,在[-a,+∞)递增,
此时f(x)的最小值为f(-a),且f(-a)=e-a(a2-a2+a)=e-a•a≤ea,解得-2≤a<0;
若a<-2,-a∈[a,+∞),f(-a)=e-a(a2-a2+a)=e-a•a≤ea,此时结论成立.
综上可得,a的取值范围是(-∞,$\frac{1}{2}$].
点评 本题考查导数的运用:求切线的斜率和单调区间、最值,考查分类讨论的思想方法,化简整理的运算能力,属于难题.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | asinθ<bsinθ | B. | absinθ<basinθ | ||
| C. | alogbsinθ<blogasinθ | D. | logasinθ<logbsinθ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
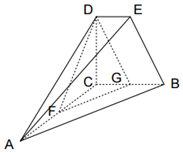 如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点.
如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日需求量n | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 频数(天) | 10 | 20 | 20 | 14 | 13 | 13 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com