
【题目】已知数列![]() ,其前
,其前![]() 项和为
项和为![]() ,满足
,满足![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
(1)若![]() ,
, ![]() ,
, ![]() (
(![]() ),求数列
),求数列![]() 的前
的前![]() 项和;
项和;
(2)若![]() ,且
,且![]() ,求证:数列
,求证:数列![]() 是等差数列.
是等差数列.
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】试题分析: ![]() 根据已知条件得到
根据已知条件得到![]() ,两式相减得
,两式相减得![]() ,得到
,得到![]() 求得
求得![]() 的值,进而得到
的值,进而得到![]() ,即可得到数列
,即可得到数列![]() 为以
为以![]() 为首项,
为首项, ![]() 为公比的等比数列,然后求得数列
为公比的等比数列,然后求得数列![]() 的前
的前![]() 项和;
项和;
![]() 将
将![]() ,且
,且![]() 代入,解得
代入,解得![]() ,
, ![]() ,猜想
,猜想![]() ,用数学归纳法证明
,用数学归纳法证明
解析:(1)![]() ,所以
,所以![]() .两式相减得
.两式相减得![]() .
.
即![]()
所以![]() ,即
,即![]() ,
,
又![]() ,所以
,所以![]() ,得
,得![]()
因此数列![]() 为以2为首项,2为公比的等比数列.
为以2为首项,2为公比的等比数列. ![]() ,前n项和为
,前n项和为![]()
(2)当n = 2时, ![]() ,
,
所以![]() . 又
. 又![]() ,可以解得
,可以解得![]() ,
, ![]()
所以![]() ,
, ![]() ,两式相减得
,两式相减得![]()
即![]() . 猜想
. 猜想![]() ,下面用数学归纳法证明:
,下面用数学归纳法证明:
① 当n = 1或2时, ![]() ,
, ![]() ,猜想成立;
,猜想成立;
② 假设当![]() (
(![]() )时,
)时, ![]() 成立
成立
则当![]() 时,
时, ![]() 猜想成立.
猜想成立.
由①、②可知,对任意正整数n, ![]() .
.
所以![]() 为常数,所以数列
为常数,所以数列![]() 是等差数列.
是等差数列.


科目:高中数学 来源: 题型:
【题目】(题文)从某校高一年级随机抽取![]() 名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
组号 | 分组 | 频数 | 频率 |
|
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
|

(Ⅰ)求![]() 的值.
的值.
(Ⅱ)若![]() ,补全表中数据,并绘制频率分布直方图.
,补全表中数据,并绘制频率分布直方图.
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,若上述数据的平均值为![]() ,求
,求![]() ,
,![]() 的值,并由此估计该校高一学生的日平均睡眠时间不少于
的值,并由此估计该校高一学生的日平均睡眠时间不少于![]() 小时的概率.
小时的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂因排污比较严重,决定着手整治,一个月时污染度为![]() ,整治后前四个月的污染度如下表:
,整治后前四个月的污染度如下表:
月数 |
|
|
|
| … |
污染度 |
|
|
|
| … |
污染度为![]() 后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:
后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:![]() ,
,![]() ,
,![]() ,其中
,其中![]() 表示月数,
表示月数,![]() 、
、![]() 、
、![]() 分别表示污染度.
分别表示污染度.
(1)问选用哪个函数模拟比较合理,并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在
,若存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点,已知函数
的不动点,已知函数![]()
(1)当![]() ,
,![]() 时,求函数
时,求函数![]() 的不动点;
的不动点;
(2)若对任意实数![]() ,函数
,函数![]() 恒有不动点,求
恒有不动点,求![]() 的取值范围;
的取值范围;
(3)在(2)条件下,若![]() 图象上的
图象上的![]() 两点的横坐标是函数
两点的横坐标是函数![]() 的不动点,且
的不动点,且![]() 的中点在直线
的中点在直线![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列命题的真假:
(1)![]() 是
是![]() 的必要条件;
的必要条件;
(2)![]() 是
是![]() 的充要条件;
的充要条件;
(3)两个三角形的两组对应角相等是这两个三角形相似的充要条件;
(4)三角形的三条边满足勾股定理是这个三角形为直角三角形的充要条件;
(5)在![]() 中,重心和垂心重合是
中,重心和垂心重合是![]() 为等边三角形的必要条件;
为等边三角形的必要条件;
(6)如果点![]() 到点
到点![]() 的距离相等,则点
的距离相等,则点![]() 一定在线段
一定在线段![]() 的垂直平分线上.
的垂直平分线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
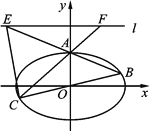
【题目】如图,在平面直角坐标系![]() 中,椭圆:
中,椭圆: ![]() 的离心率为
的离心率为![]() ,直线l:y=2上的点和椭圆上的点的距离的最小值为1.
,直线l:y=2上的点和椭圆上的点的距离的最小值为1.
(Ⅰ) 求椭圆的方程;
(Ⅱ) 已知椭圆的上顶点为A,点B,C是上的不同于A的两点,且点B,C关于原点对称,直线AB,AC分别交直线l于点E,F.记直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
, ![]() .
.
① 求证: ![]() 为定值;
为定值;
② 求△CEF的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上周某校高三年级学生参加了数学测试,年级组织任课教师对这次考试进行成绩分析现从中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组;第二组;……;第六组,并据此绘制了如图所示的频率分布直方图.
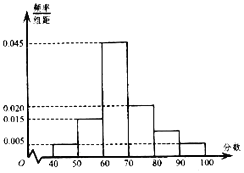
(1)估计这次月考数学成绩的平均分和众数;
(2)从成绩大于等于80分的学生中随机选2名,求至少有1名学生的成绩在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“冰桶挑战赛”是一项社交网络上发起的慈善公益活动,活动规定:被邀请者要么在![]() 小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外
小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外![]() 个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
(1)若某参与者接受挑战后,对其他![]() 个人发出邀请,则这
个人发出邀请,则这![]() 个人中至少有
个人中至少有![]() 个人接受挑战的概率是多少?
个人接受挑战的概率是多少?
(2)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构进行了随机抽样调查,调查得到如下列联表:
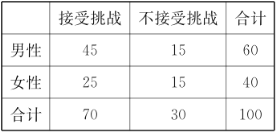
根据表中数据,能否有![]() %的把握认为“冰桶挑战赛与受邀者的性别有关”?
%的把握认为“冰桶挑战赛与受邀者的性别有关”?
附: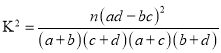

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com