
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其过点
,其过点![]() ,其长轴的左右两个端点分别为
,其长轴的左右两个端点分别为![]() ,直线
,直线![]() 交椭圆于两点
交椭圆于两点![]() .
.
(1)求椭圆的标准方程;
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由椭圆的离心率为![]() ,且过点
,且过点![]() ,列出方程组,求出
,列出方程组,求出![]() ,由此能求出椭圆方程;(2)联立方程
,由此能求出椭圆方程;(2)联立方程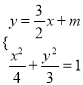 ,得
,得![]() ,由此利用根的判别式、韦达定理、直线方程,结合已知条件能求出
,由此利用根的判别式、韦达定理、直线方程,结合已知条件能求出![]() 的值.
的值.
试题解析:(1)由题意的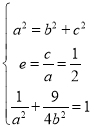 ,解得
,解得![]() ,
,
所以椭圆的方程为![]() .
.
(2)设![]() ,联立方程
,联立方程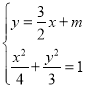 ,得
,得![]() ,
,
所以判别式![]() ,
,
因为![]() ,
,
由题意知![]() ,所以
,所以![]() ,
,
因为![]() ,即
,即![]() ,得
,得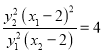 ,
,
又![]() ,所以
,所以![]() ,同理
,同理![]() ,
,
代入上式,解得![]() ,即
,即![]() ,
,
所以![]() ,解得
,解得![]() ,
,
又因为![]() ,所以
,所以![]() (舍去),所以
(舍去),所以![]() .
.
【方法点晴】本题主要考查待定系数求椭圆方程、韦达定理以及直线与椭圆的位置关系,属于难题.用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在![]() 轴上,还是在
轴上,还是在![]() 轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程
轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程![]() 或
或![]() ;③找关系:根据已知条件,建立关于
;③找关系:根据已知条件,建立关于![]() 、
、![]() 、
、![]() 的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
的方程组;④得方程:解方程组,将解代入所设方程,即为所求.


科目:高中数学 来源: 题型:
【题目】为了增强市民的环境保护组织,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织,现按年龄把该组织的成员分成5组:[20,25),[25,30),[30,35),[35,40),[40,45]. 得到的频率分布直方图如图所示,已知该组织的成员年龄在[35,40)内有20人 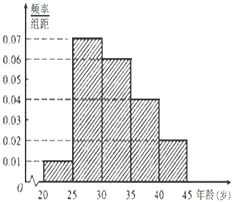
(1)求该组织的人数;
(2)若从该组织年龄在[20,25),[25,30),[30,35)内的成员中用分层抽样的方法共抽取14名志愿者参加某社区的宣传活动,问应各抽取多少名志愿者?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x+1)的定义域是[﹣1,3],则y=f(x2)的定义域是( )
A.[0,4]
B.[0,16]
C.[﹣2,2]
D.[1,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 并且满足2Sn=an2+n,an>0(n∈N*).
(1)求a1 , a2 , a3;
(2)猜想{an}的通项公式,并加以证明;
(3)设x>0,y>0,且x+y=1,证明: ![]() ≤
≤ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C: ![]() ,点A,B分别是左、右顶点,过右焦点F的直线MN(异于x轴)交于椭圆C于M、N两点.
,点A,B分别是左、右顶点,过右焦点F的直线MN(异于x轴)交于椭圆C于M、N两点.
(1)若椭圆C过点 ,且右准线方程为
,且右准线方程为![]() ,求椭圆C的方程;
,求椭圆C的方程;
(2)若直线BN的斜率是直线AM斜率的2倍,求椭圆C的离心率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率低于40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.0.35
B.0.25
C.0.20
D.0.15
查看答案和解析>>
科目:高中数学 来源: 题型:
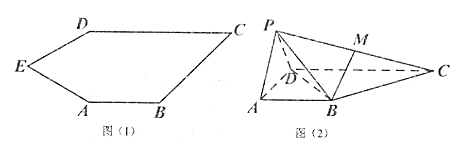
【题目】如图(1)五边形![]() 中,
中, ![]()
![]() ,将
,将![]() 沿
沿![]() 折到
折到![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() ,如图(2),点
,如图(2),点![]() 为线段
为线段![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若四棱柱![]() 的体积为
的体积为![]() ,求四面体
,求四面体![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com