
| A. | $\frac{1}{5}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{15}$ | D. | $\frac{1}{3}$ |
分析 利用列举法,确定基本事件,即可得出结论.
解答 解:不妨设3双皮鞋为a,b,c,且分别由a1、a2,b1、b2,c1、c2组成,则从中任意抽取两只的情况为
(a1,a2),(a1,b1),(a1,b2),(a1,c1),(a1,c2),(a2,b1),(a2,b2),(a2,c1),(a2,c2),(b1,b2),(b1,c1),(b1,c2),(b2,c1),(b2,c2),(c1,c2)
共15种情况,而恰为一双鞋的情况共3种,所以所求概率为P=$\frac{3}{15}$=$\frac{1}{5}$.
故选:A.
点评 本题考查古典概型的概率计算,考查学生的计算能力,确定基本事件是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
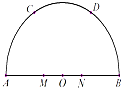 如图AB是半圆O的直径,C,D是弧$\widehat{AB}$的三等分点,M,N是线段AB的三等分点,若OA=6,则$\overrightarrow{MC}•\overrightarrow{ND}$=( )
如图AB是半圆O的直径,C,D是弧$\widehat{AB}$的三等分点,M,N是线段AB的三等分点,若OA=6,则$\overrightarrow{MC}•\overrightarrow{ND}$=( )| A. | 18 | B. | 8 | C. | 26 | D. | 35 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,2) | B. | (-∞,2) | C. | (-∞,-2)∪(2,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com