
分析 由已知中奇函数f(x)在定义域[-2,2]内递减,我们可将f(1-m)+f(1-m2)<0转化为一个关于实数m的不等式组,解不等式组,即可得到实数m的取值范围.
解答 解:由f(1-m)+f(1-m2)<0,得f(1-m)<-f(1-m2).
又∵f(x)为奇函数,∴f(1-m)<f(m2-1).
∵f(x)在定义域[-2,2]上单调递减$\left\{\begin{array}{l}{-2≤1-m≤2}\\{-2≤1-{m}^{2}≤2}\\{1-m>{m}^{2}-1}\end{array}\right.$,解得-1≤m<1
∴实数m 的取值范围为[-1,1).
点评 本题考查的知识点是函数单调性的性质,其中根据函数的单调性将f(1-m)+f(1-m2)<0转化为一个关于实数m的不等式组是解答本题的关键,但解答本题时易忽略函数的定义域而造成错误.


科目:高中数学 来源: 题型:解答题
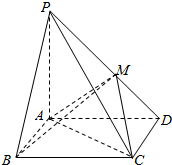 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2>b2 | B. | ac>bc | C. | $\frac{1}{a}<\frac{1}{b}$ | D. | ac2≥bc2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com