
【题目】设函数![]() .
.
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若当![]() 时
时![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1) f(x)在(-∞,0)单调减少,在(0,+∞)单调增加;(2) a的取值范围为(-∞,![]() ].
].
【解析】
(1)a=0时,f(x)=ex-1-x,f′(x)=ex-1.分别令f′(x)<0,f′(x)>0
可求![]() 的单调区间;
的单调区间;
(2求导得到)f′(x)=ex-1-2ax.由(1)知ex≥1+x,当且仅当x=0时等号成立.故问题转化为f′(x)≥x-2ax=(1-2a)x,从而对1-2a的符号进行讨论即可得出结果.
(1)a=0时,f(x)=ex-1-x,f′(x)=ex-1.
当x∈(-∞,0)时,f′(x)<0;当x∈(0,+∞)时,f′(x)>0.故f(x)在(-∞,0)单调减少,在(0,+∞)单调增加
(2)f′(x)=ex-1-2ax.由(1)知ex≥1+x,当且仅当x=0时等号成立.故f′(x)≥x-2ax=(1-2a)x,从而当1-2a≥0,即a≤![]() 时,f′(x)≥0(x≥0),而f(0)=0,于是当x≥0时,f(x)≥0.由ex>1+x(x≠0)得e-x>1-x(x≠0),从而当a>
时,f′(x)≥0(x≥0),而f(0)=0,于是当x≥0时,f(x)≥0.由ex>1+x(x≠0)得e-x>1-x(x≠0),从而当a>![]() 时,f′(x)<ex-1+2a(e-x-1)=e-x(ex-1)(ex-2a),故当x∈(0,ln2a)时, f′(x)<0,而f(0)=0,于是当x∈(0,ln2a)时,f(x)<0,
时,f′(x)<ex-1+2a(e-x-1)=e-x(ex-1)(ex-2a),故当x∈(0,ln2a)时, f′(x)<0,而f(0)=0,于是当x∈(0,ln2a)时,f(x)<0,
综上可得a的取值范围为(-∞,![]() ].
].


科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点
,以极点![]() 为直角坐标原点,以极轴为
为直角坐标原点,以极轴为![]() 轴的正半轴建立平面直角坐标系
轴的正半轴建立平面直角坐标系![]() ,将曲线
,将曲线![]() 向左平移
向左平移![]() 个单位长度,再将得到的曲线上的每一个点的横坐标缩短为原来的
个单位长度,再将得到的曲线上的每一个点的横坐标缩短为原来的![]() ,纵坐标保持不变,得到曲线
,纵坐标保持不变,得到曲线![]()
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),点
为参数),点![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到直线
到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴与短轴比值是2,椭圆C过点
的长轴与短轴比值是2,椭圆C过点![]() .
.
(1)求椭圆C的标准方程;
(2)过点![]() 作圆x2+y2=1的切线
作圆x2+y2=1的切线![]() 交椭圆C于A,B两点,记△AOB(O为坐标原点)的面积为S△AOB,将S△AOB表示为m的函数,并求S△AOB的最大值
交椭圆C于A,B两点,记△AOB(O为坐标原点)的面积为S△AOB,将S△AOB表示为m的函数,并求S△AOB的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天津市某学校组织教师进行“学习强国”知识竞赛,规则为:每位参赛教师都要回答3个问题,且对这三个问题回答正确与否相互之间互不影响,若每答对1个问题,得1分;答错,得0分,最后按照得分多少排出名次,并分一、二、三等奖分别给予奖励.已知对给出的3个问题,教师甲答对的概率分别为![]() ,
,![]() ,p.若教师甲恰好答对3个问题的概率是
,p.若教师甲恰好答对3个问题的概率是![]() ,则
,则![]() ________;在前述条件下,设随机变量X表示教师甲答对题目的个数,则X的数学期望为________.
________;在前述条件下,设随机变量X表示教师甲答对题目的个数,则X的数学期望为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着生活水平的提高和人们对健康生活的重视,越来越多的人加入到健身运动中.国家统计局数据显示,2019年有4亿国人经常参加体育锻炼.某健身房从参与健身的会员中随机抽取100人,对其每周参与健身的天数和2019年在该健身房所有消费金额(单位:元)进行统计,得到以下统计表及统计图:
平均每周健身天数 | 不大于2 | 3或4 | 不少于5 |
人数(男) | 20 | 35 | 9 |
人数(女) | 10 | 20 | 6 |

若某人平均每周进行健身天数不少于5,则称其为“健身达人”.该健身房规定消费金额不多于1600元的为普通会员,超过1600元但不超过3200元的为银牌会员,超过3200元的为金牌会员.
(1)已知金牌会员都是健身达人,现从健身达人中随机抽取2人,求他们均是金牌会员的概率;
(2)能否在犯错误的概率不超过![]() 的前提下认为性别和是否为“健身达人”有关系?
的前提下认为性别和是否为“健身达人”有关系?
(3)该健身机构在2019年年底针对这100位消费者举办一次消费返利活动,现有以下两种方案:
方案一:按分层抽样从普通会员、银牌会员和金牌会员中共抽取25位“幸运之星”,分别给予188元,288元,888元的幸运奖励;
方案二:每位会员均可参加摸奖游戏,游戏规则如下:摸奖箱中装有5张形状大小完全一样的卡片,其中3张印跑步机图案、2张印动感单车图案,有放回地摸三次卡片,每次只能摸一张,若摸到动感单车的总数为2,则获得100元奖励,若摸到动感单车的总数为3,则获得200元奖励,其他情况不给予奖励.规定每个普通会员只能参加1次摸奖游戏,每个银牌会员可参加2次摸奖游戏,每个金牌会员可参加3次摸奖游戏(每次摸奖结果相互独立).
请你比较该健身房采用哪一种方案时,在此次消费返利活动中的支出较少,并说明理由.
附: ,其中
,其中![]() 为样本容量.
为样本容量.
| 0.50 | 0.25 | 0.10 | 0.05 | 0.010 | 0.005 |
| 0.455 | 1.323 | 2.706 | 3.841 | 6.636 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】约公元前600年,几何学家泰勒斯第一个测出了金字塔的高度.如图,金字塔是正四棱锥,泰勒斯先测量出某个金字塔的底棱长约为230米;然后,他站立在沙地上,请人不断测量他的影子,当他的影子和身高相等时,他立刻测量出该金字塔影子的顶点A与相应底棱中点B的距离约为22.2米.此时,影子的顶点A和底面中心O的连线恰好与相应的底棱垂直,则该金字塔的高度约为( )
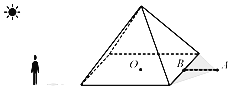
A.115米B.137.2米C.230米D.252.2米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )

A. 甲的极差是29 B. 甲的中位数是24
C. 甲罚球命中率比乙高 D. 乙的众数是21
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 对任意的
对任意的![]() ,均有
,均有![]() ,则称函数
,则称函数![]() 具有性质
具有性质![]() .
.
(1)判断下面两个函数是否具有性质![]() ,并说明理由.①
,并说明理由.①![]() ;②
;②![]() .
.
(2)若函数![]() 具有性质
具有性质![]() ,且
,且![]() ,求证:对任意
,求证:对任意![]() 有
有![]() ;
;
(3)在(2)的条件下,是否对任意![]() 均有
均有![]() .若成立给出证明,若不成立给出反例.
.若成立给出证明,若不成立给出反例.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com