
【题目】设函数 ![]() ,其中[x]表示不超过x的最大整数,若直线y=kx+k(k>0)与函数y=f(x)的图象恰有三个不同的交点,则k的取值范围是 .
,其中[x]表示不超过x的最大整数,若直线y=kx+k(k>0)与函数y=f(x)的图象恰有三个不同的交点,则k的取值范围是 .
【答案】[ ![]() ,
, ![]() )
)
【解析】解:∵函数 ![]() , ∴函数的图象如下图所示:
, ∴函数的图象如下图所示: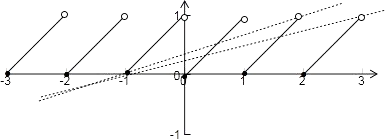
∵y=kx+k=k(x+1),故函数图象一定过(﹣1,0)点
若f(x)=kx+k有三个不同的根,
则y=kx+k与y=f(x)的图象有三个交点
当y=kx+k过(2,1)点时,k= ![]() ,
,
当y=kx+k过(3,1)点时,k= ![]() ,
,
故f(x)=kx+k有三个不同的根,则实数k的取值范围是[ ![]() ,
, ![]() )
)
【考点精析】解答此题的关键在于理解函数的零点与方程根的关系的相关知识,掌握二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.


科目:高中数学 来源: 题型:
【题目】一个函数f(x),如果对任意一个三角形,只要它的三边长a,b,c都在f(x)的定义域内,就有f(a),f(b),f(c)也是某个三角形的三边长,则称f(x)为“三角保型函数”,给出下列函数: ①f(x)= ![]() ;②f(x)=x2;③f(x)=2x;④f(x)=lgx,
;②f(x)=x2;③f(x)=2x;④f(x)=lgx,
其中是“三角保型函数”的是( )
A.①②
B.①③
C.②③④
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为R,它的导函数y=f′(x)的部分图象如图所示,则下面结论正确的是( ) 
A.在(1,2)上函数f(x)为增函数
B.在(3,4)上函数f(x)为减函数
C.在(1,3)上函数f(x)有极大值
D.x=3是函数f(x)在区间[1,5]上的极小值点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,g(x)=2ln(x+m).
,g(x)=2ln(x+m).
(1)当m=0,存在x0∈[ ![]() ,e](e为自然对数的底数),使
,e](e为自然对数的底数),使 ![]() ,求实数a的取值范围;
,求实数a的取值范围;
(2)当a=m=1时,设H(x)=xf(x)+g(x),在H(x)的图象上是否存在不同的两点A(x1 , y1),B(x2 , y2)(x1>x2>﹣1),使得H(x1)﹣H(x2)= ![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】偶函数y=f(x)在区间(﹣∞,﹣1]上是增函数,则下列不等式成立的是( )
A.f(﹣1)>f( ![]() )
)
B.f( ![]() )>f(﹣
)>f(﹣ ![]() )??
)??
C.f(4)>f(3)
D.f(﹣ ![]() )>f(
)>f( ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一条笔直公路上有A,B两地,甲骑自行车从A地到B地,乙骑着摩托车从B地到A地,到达A地后立即按原路返回,如图是甲乙两人离A地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数图象,根据图象解答以下问题:
之间的函数图象,根据图象解答以下问题:
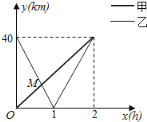
![]() 直接写出
直接写出![]() ,
,![]() 与x之间的函数关系式
与x之间的函数关系式![]() 不必写过程
不必写过程![]() ,求出点M的坐标,并解释该点坐标所表示的实际意义;
,求出点M的坐标,并解释该点坐标所表示的实际意义;
![]() 若两人之间的距离不超过5km时,能够用无线对讲机保持联系,求在乙返回过程中有多少分钟甲乙两人能够用无线对讲机保持联系;
若两人之间的距离不超过5km时,能够用无线对讲机保持联系,求在乙返回过程中有多少分钟甲乙两人能够用无线对讲机保持联系;
![]() 若甲乙两人离A地的距离之积为
若甲乙两人离A地的距离之积为![]() ,求出函数
,求出函数![]() 的表达式,并求出它的最大值.
的表达式,并求出它的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四人进行选择题解题比赛,已知每个选择题选择正确得![]() 分,否则得
分,否则得![]() 分.其测试结果如下:甲解题正确的个数小于乙解题正确的个数,乙解题正确的个数小于丙解题正确的个数,丙解题正确的个数小于丁解题正确的个数;且丁解题正确的个数的
分.其测试结果如下:甲解题正确的个数小于乙解题正确的个数,乙解题正确的个数小于丙解题正确的个数,丙解题正确的个数小于丁解题正确的个数;且丁解题正确的个数的![]() 倍小于甲解题正确的个数的
倍小于甲解题正确的个数的![]() 倍,则这四人测试总得分数最少为( )
倍,则这四人测试总得分数最少为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考察某种药物预防疾病的效果,进行动物试验,调查了 105 个样本,统计结果为:服药的共有 55 个样本,服药但患病的仍有 10 个样本,没有服药且未患病的有 30个样本.
(1)根据所给样本数据完成 ![]() 列联表中的数据;
列联表中的数据;
(2)请问能有多大把握认为药物有效?
(参考公式:![]() 独立性检验临界值表
独立性检验临界值表
概率 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
患病 | 不患病 | 合计 | |
服药 | |||
没服药 | |||
合计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com