
【题目】已知二次函数f(x)=x2+bx+c,若对任意的x1,x2∈[-1,1],有|f(x1)-f(x2)|≤6,则b的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABC﹣DEF中,已知平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3,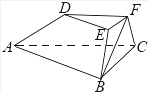
(1)求证:EF⊥平面ACFD;
(2)求二面角B﹣AD﹣F的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )
A.7
B.12
C.17
D.34
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 关于
关于![]() 轴对称,顶点在坐标原点
轴对称,顶点在坐标原点![]() ,直线
,直线![]() 经过抛物线
经过抛物线![]() 的焦点.
的焦点.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)若不经过坐标原点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,且满足
,且满足![]() ,证明直线
,证明直线![]() 过
过![]() 轴上一定点
轴上一定点![]() ,并求出点
,并求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=3,an+1=![]() +2(n∈N*).
+2(n∈N*).
(Ⅰ)计算a2,a3,a4的值;
(Ⅱ)根据计算结果猜想{an}的通项公式,并用数学归纳法加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义域为R的偶函数,f(-1)=3,且当x≥0时,f(x)=2x+x+c(c是常数),则不等式f(x-1)<6的解集是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系内从点P1(0,0)作x轴的垂线交曲线y=ex于点Q1(0,1),曲线在Q1点处的切线与x轴交于点P2.再从P2作x轴的垂线交曲线于点Q2,依次重复上述过程得到一系列点:P1,Q1;P2,Q2;…;Pn,Qn,记![]() 点的坐标为(
点的坐标为(![]() ,0)(k=1,2,…,n).
,0)(k=1,2,…,n).

(1)试求![]() 与
与![]() 的关系(k=2,…,n);
的关系(k=2,…,n);
(2)求|P1Q1|+|P2Q2|+|P3Q3|+…+|PnQn|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建坐标系,已知曲线![]() ,已知过点
,已知过点![]() 的直线的参数方程为:
的直线的参数方程为: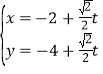 (t为参数),直线与曲线C分别交于M,N.
(t为参数),直线与曲线C分别交于M,N.
(Ⅰ)写出曲线C和直线的普通方程;
(Ⅱ)若![]() 成等比数列,求a的值.
成等比数列,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com