
【题目】已知函数f(x)= 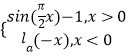 (a>0,且a≠1)的图象上关于y轴对称的点至少有5对,则实数a的取值范围是( )
(a>0,且a≠1)的图象上关于y轴对称的点至少有5对,则实数a的取值范围是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.( ![]() ,1)
,1)
D.(0, ![]() )
)
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】为做好2022年北京冬季奥运会的宣传工作,组委会计划从某大学选取若干大学生志愿者,某记者在该大学随机调查了1000名大学生,以了解他们是否愿意做志愿者工作,得到的数据如表所示:
愿意做志愿者工作 | 不愿意做志愿者工作 | 合计 | |
男大学生 | 610 | ||
女大学生 | 90 | ||
合计 | 800 |
(1)根据题意完成表格;
(2)是否有![]() 的把握认为愿意做志愿者工作与性别有关?
的把握认为愿意做志愿者工作与性别有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某厂生产某种产品的过程中记录的几组数据,其中![]() 表示产量(单位:吨),
表示产量(单位:吨),![]() 表示生产中消耗的煤的数量(单位:吨).
表示生产中消耗的煤的数量(单位:吨).
|
|
|
|
|
|
|
|
|
|
|
|
(1)试在给出的坐标系下作出散点图,根据散点图判断,在![]() 与
与![]() 中,哪一个方程更适合作为变量
中,哪一个方程更适合作为变量![]() 关于
关于![]() 的回归方程模型?(给出判断即可,不需要说明理由)
的回归方程模型?(给出判断即可,不需要说明理由)
(2)根据(1)的结果以及表中数据,建立变量![]() 关于
关于![]() 的回归方程.并估计生产
的回归方程.并估计生产![]() 吨产品需要准备多少吨煤.参考公式:
吨产品需要准备多少吨煤.参考公式: .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+|x+2|.
(1)当a=1 时,求不等式f(x)≤5的解集;
(2)x0∈R,f(x0)≤|2a+1|,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有6个人排成一排照相,由于甲乙性格不合,所以要求甲乙不相邻,丙最高,要求丙站在最中间的两个位置中的一个位置上,则不同的站法有( )种.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构为了研究人的脚的大小与身高之间的关系,随机测量了20人,得到如下数据:


(1) 若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”;“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”,请根据上表数据完成下面的2×2列联表.

(2)根据(1)中的2×2列联表,在犯错误的概率不超过0.01的前提下,能否认为脚的大小与身高之间有关系?
![]() ,
,
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个小组各10名学生的英语口语测试成绩如下(单位:分).
甲组:76,90,84,86,81,87,86,82,85,83 乙组:82,84,85,89,79,80,91,89,79,74
现从这20名学生中随机抽取一人,将“抽出的学生为甲组学生”记为事件A;“抽出学生的英语口语测试成绩不低于85分”记为事件B,则P(AB)、P(A|B)的值分别是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com