
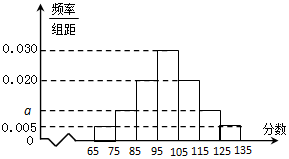
 某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图:
某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图:分析 (1)由频率和为1列出方程求出a的值,再计算平均数;
(2)由频率分布直方图计算学生成绩在105分以上的频率与频数.
解答 解:(1)由频率分布直方图可知:
(0.005×2+2a+0.020×2+0.030)×10=1,
∴a=0.010;…(3分)
平均数为$\overline{x}$=(70×0.005+80×0.010+90×0.020+100×0.030
+110×0.020+120×0.010+130×0.005)×10=100分;…(7分)
(2)由频率分布直方图可知:
学生成绩在105分以上的频率为
(0.020+0.010+0.005)×10=0.35;
∴该校高二1000名学生中,数学成绩在105分以上的大约有
1000×0.35=350人.…(12分)
点评 本题考查了频率分布直方图与频率、频数、平均数的计算问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
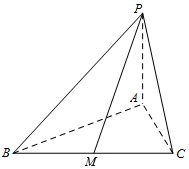 在三棱锥P-ABC中,底面ABC是边长为6的正三角形,PA⊥底面ABC,且PB与底面ABC所成的角为$\frac{π}{6}$.
在三棱锥P-ABC中,底面ABC是边长为6的正三角形,PA⊥底面ABC,且PB与底面ABC所成的角为$\frac{π}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有一个白球;至少有一个红球 | B. | 至少有一个白球;红、黑球各一个 | ||
| C. | 恰有一个白球;一个白球一个黑球 | D. | 至少有一个白球;都是白球 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{2}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
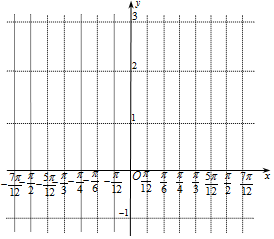 某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:
某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:| 2x-$\frac{π}{3}$ | -$\frac{4}{3}$π | -π | -$\frac{π}{2}$ | 0 | $\frac{π}{2}$ | $\frac{2}{3}$π |
| x | -$\frac{π}{2}$ | -$\frac{π}{3}$ | -$\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{π}{2}$ |
| f(x) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com