
求下列各函数的导数:
(1)y=(x+1)(x+2)(x+3).
(2)y=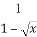 +
+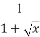 .
.
(3)y=e-xsin2x.
(1) y'=3x2+12x+11 (2) y'=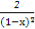 . (3) y' =e-x(2cos2x-sin2x).
. (3) y' =e-x(2cos2x-sin2x).
【解析】(1)方法一:y=(x2+3x+2)(x+3)=x3+6x2+11x+6,∴y'=3x2+12x+11.
方法二:y'=[(x+1)(x+2)]'(x+3)+(x+1)(x+2)·(x+3)'
=[(x+1)'(x+2)+(x+1)(x+2)'](x+3)+(x+1)·(x+2)
=(x+2+x+1)(x+3)+(x+1)(x+2)
=(2x+3)(x+3)+(x+1)(x+2)
=3x2+12x+11.
(2)∵y= +
+ =
= ,
,
∴y'=( )'=
)'= =
=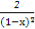 .
.
(3)y'=(-e-x)sin2x+e-x(cos2x)×2
=e-x(2cos2x-sin2x).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十六第二章第十三节练习卷(解析版) 题型:选择题
如图,函数y=-x2+2x+1与y=1相交形成一个闭合图形(图中的阴影部分),则该闭合图形的面积是( )

(A)1 (B) (C)
(C) (D)2
(D)2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十二第二章第九节练习卷(解析版) 题型:解答题
某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)= x2+10x(万元).当年产量不小于80千件时,C(x)=51x+
x2+10x(万元).当年产量不小于80千件时,C(x)=51x+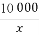 -1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
-1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式.
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十九第三章第三节练习卷(解析版) 题型:选择题
函数y=3cos(x+φ)+2的图象关于直线x= 对称,则|φ|的最小值是( )
对称,则|φ|的最小值是( )
(A) (B)
(B)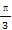 (C)
(C)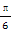 (D)
(D)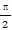
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十九第三章第三节练习卷(解析版) 题型:选择题
已知函数f(x)=3cos(2x- )在[0,
)在[0,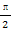 ]上的最大值为M,最小值为m,则M+m等于( )
]上的最大值为M,最小值为m,则M+m等于( )
(A)0 (B)3+
(C)3- (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十三第二章第十节练习卷(解析版) 题型:选择题
如图,其中有一个是函数f(x)= x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函数f′(x)的图象,则f(-1)为( )
x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函数f′(x)的图象,则f(-1)为( )
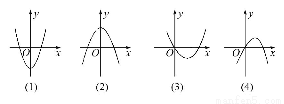
(A)2 (B)- (C)3 (D)-
(C)3 (D)-
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十一第二章第八节练习卷(解析版) 题型:填空题
若函数f(x)=(m-1)x2+2(m+1)x-1有且仅有一个零点,则实数m的取值集合是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十六第十章第三节练习卷(解析版) 题型:填空题
若(x+ )n的展开式中第3项与第7项的二项式系数相等,则该展开式中
)n的展开式中第3项与第7项的二项式系数相等,则该展开式中 的系数为 .
的系数为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com