
分析 由直线ax-by+8=0(a>0,b>0)经过x2+y2+4x-4y=0的圆心,可得a+b=4,则$\frac{1}{a}$+$\frac{1}{b}$=$\frac{1}{4}$($\frac{1}{a}$+$\frac{1}{b}$)(a+b)=$\frac{1}{4}$(2+$\frac{b}{a}+\frac{a}{b}$),再用基本不等式求最小值.
解答 解:∵圆x2+y2+4x-4y=0的圆心坐标是(-2,2),
直线ax-by+8=0过圆心,∴a+b=4,
∴$\frac{1}{a}$+$\frac{1}{b}$=$\frac{1}{4}$($\frac{1}{a}$+$\frac{1}{b}$)(a+b)=$\frac{1}{4}$(2+$\frac{b}{a}+\frac{a}{b}$)≥1,
当b=a=2时取等号.
故$\frac{1}{a}$+$\frac{1}{b}$的最小值为1,
故答案为1.
点评 本题考查了基本不等式的应用,考查了圆的一般式方程,解题的关键是得出a+b=4.


科目:高中数学 来源: 题型:选择题
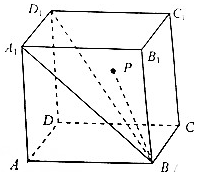 在正方体ABCD-A1B1C1D1中,点P在CDD1C1所在的平面上,满足∠PBD1=∠A1BD1,则动点P的轨迹是( )
在正方体ABCD-A1B1C1D1中,点P在CDD1C1所在的平面上,满足∠PBD1=∠A1BD1,则动点P的轨迹是( )| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,0] | B. | (-3,1] | C. | [-1,3)∪(3,+∞) | D. | [-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-y+1=0 | B. | 2x-y-4=0 | C. | x+2y-2=0 | D. | x+2y-4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{5\sqrt{42}}}{2}$ | B. | $5\sqrt{42}$ | C. | $5\sqrt{3}$ | D. | $5\sqrt{14}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $\frac{33}{2}$ | D. | $\frac{33}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com