练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知{an}是各项为正数的等比数列，{bn}是等差数列，且a1=b1=1，b2+b3=2a3 ， a5﹣3b2=7．
    （1）求{an}和{bn}的通项公式；
    （2）设cn=anbn ， n∈N* ， 求数列{cn}的前n项和为Sn ．

    【答案】
    （1）解：设{an}的公比为q，{bn}的公差为d，由题意q＞0，

    由已知，有 ，

    消去d得q4﹣2q2﹣8=0，解得q=2，d=2，

    所以{an}的通项公式为 ，{bn}的通项公式为 ．


    （2）解：由（1）有 ，设{cn}的前n项和为Sn，

    则 ，

    ，

    两式相减得 ，

    所以 ．


    【解析】（1）根据等比数列，等差数列的通项公式，由题意列出等式解出公比q，公差d，即可得出通项公式，（2）由（1）中的通项公式表示出cn，使用错位相减即可求出Sn.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设a1 ， a2 ， …，an是1，2，…，n的一个排列，求证： ·

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a＞2，求证：loga(a－1)＜log(a＋1)a.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱A1B1C1﹣ABC中，AB=AC=AA1 ， ，点D是BC的中点．
    （I）求证：AD⊥平面BCC1B1；
    （II）求证：A1B∥平面ADC1；
    （III）求二面角A﹣A1B﹣D的余弦值．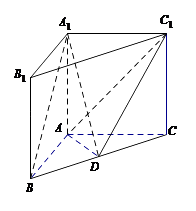

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=﹣ +4x﹣3lnx在[t，t+1]上不单调，则t的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）= ，关于x的方程[f（x）]2+mf（x）﹣1=0有三个不同的实数解，则实数m的取值范围是（ ）
    A.（﹣∞，e﹣ ）
    B.（e﹣ ，+∞）
    C.（0，e）
    D.（1，e）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司为对本公司的160名员工的身体状况进行调查，先将员工随机编号为1，2，3，…，159，160，采用系统抽样的方法（等间距地抽取，每段抽取一个个体）将抽取的一个样本．已知抽取的员工中最小的两个编号为5，21，那么抽取的员工中，最大的编号应该是（ ）
    A.141
    B.142
    C.149
    D.150

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知{an}是等差数列，其中a10=30，a20=50．
    （1）求数列{an}的通项公式；
    （2）若bn=an﹣20，求数列{bn}的前n项和Tn的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】等比数列{an}中，已知a1=2，a4=16．
    （1）求数列{an}的通项公式an；
    （2）若a3 ， a5分别是等差数列{bn}的第4项和第16项，求数列{bn}的通项公式及前n项和Sn ．

    查看答案和解析>>

    同步练习册答案