
【题目】
已知点![]() ,
,![]() ,动点P满足
,动点P满足![]() ,记动点P的轨迹为W.
,记动点P的轨迹为W.
(Ⅰ)求W的方程;
(Ⅱ)直线![]() 与曲线W交于不同的两点C,D,若存在点
与曲线W交于不同的两点C,D,若存在点![]() ,使得
,使得![]() 成立,求实数m的取值范围.
成立,求实数m的取值范围.
【答案】(Ⅰ)![]() . (Ⅱ)
. (Ⅱ)![]() .
.
【解析】
试题(Ⅰ)依题意,点P到两定点A、B的距离之和为定值![]() ,且此值大于两定点间的距离2,由椭圆定义可知动点P的轨迹是以A,B为焦点,长轴长为
,且此值大于两定点间的距离2,由椭圆定义可知动点P的轨迹是以A,B为焦点,长轴长为![]() 的椭圆,从而写出W的标准方程;
的椭圆,从而写出W的标准方程;
(Ⅱ)先将直线方程与曲线W的方程联立,得关于x的一元二次方程,利用韦达定理,写出交点C、D的横坐标的和与积,再求出线段CD的中垂线的方程,此直线与x轴的交点即为M,从而得m关于k的函数,求函数值域即可
试题解析:(Ⅰ)由椭圆的定义可知,动点P的轨迹是以A,B为焦点,长轴长为![]() 的椭圆.
的椭圆.
∴![]() ,
,![]() ,
,![]() .
.
W的方程是![]() .
.
(Ⅱ)设C,D两点坐标分别为![]() 、
、![]() ,C,D中点为
,C,D中点为![]() .
.
由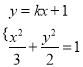 得
得![]() .
.
所以![]()
∴![]() , 从而
, 从而![]() .
.
∴![]() 斜率
斜率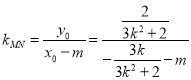 .
.
又∵![]() , ∴
, ∴![]() ,∴
,∴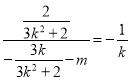 即
即![]()
当![]() 时,
时,![]() ;
;
当![]() 时,
时,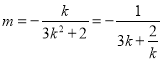
![]() .
.
故所求![]() 的取范围是
的取范围是![]() .
.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系下,方程![]() 的图形为如图所示的“幸运四叶草”,又称为玫瑰线.
的图形为如图所示的“幸运四叶草”,又称为玫瑰线.
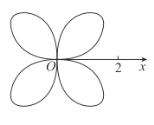
(1)当玫瑰线的![]() 时,求以极点为圆心的单位圆与玫瑰线的交点的极坐标;
时,求以极点为圆心的单位圆与玫瑰线的交点的极坐标;
(2)求曲线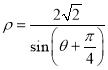 上的点M与玫瑰线上的点N距离的最小值及取得最小值时的点M、N的极坐标(不必写详细解题过程).
上的点M与玫瑰线上的点N距离的最小值及取得最小值时的点M、N的极坐标(不必写详细解题过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,已知直线l的参数方程为: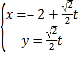 ,
,![]() 为参数
为参数![]() 点的极坐标为
点的极坐标为![]() ,曲线C的极坐标方程为
,曲线C的极坐标方程为![]() .
.
![]() Ⅰ
Ⅰ![]() 试将曲线C的极坐标方程化为直角坐标方程,并求曲线C的焦点在直角坐标系下的坐标;
试将曲线C的极坐标方程化为直角坐标方程,并求曲线C的焦点在直角坐标系下的坐标;
![]() Ⅱ
Ⅱ![]() 设直线l与曲线C相交于两点A,B,点M为AB的中点,求
设直线l与曲线C相交于两点A,B,点M为AB的中点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知椭圆![]() 上任意一点到其两个焦点
上任意一点到其两个焦点![]() ,
,![]() 的距离之和等于
的距离之和等于![]() ,焦距为2c,圆
,焦距为2c,圆![]() ,
,![]() ,
,![]() 是椭圆的左、右顶点,AB是圆O的任意一条直径,四边形
是椭圆的左、右顶点,AB是圆O的任意一条直径,四边形![]() 面积的最大值为
面积的最大值为![]() .
.
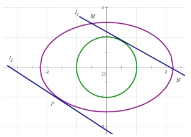
(1)求椭圆C的方程;
(2)如图,若直线![]() 与圆O相切,且与椭圆相交于M,N两点,直线
与圆O相切,且与椭圆相交于M,N两点,直线![]() 与
与![]() 平行且与椭圆相切于P(O,P两点位于
平行且与椭圆相切于P(O,P两点位于![]() 的同侧),求直线
的同侧),求直线![]() ,
,![]() 距离d的取值范围.
距离d的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市旅游局为了进一步开发旅游资源,需要了解游客的情况,以便制定相应的策略,在某月中随机抽取甲、乙两个景点各10天的游客数,画出茎叶图如下:若景点甲中的数据的中位数是126,景点乙中的数据的平均数是124.
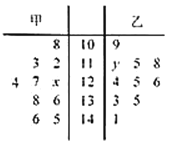
(1)求![]() ,
,![]() 的值;
的值;
(2)若将图中景点甲中的数据作为该景点较长一段时期内的样本数据(视样本频率为概率).今从这段时期内任取4天,记其中游客数不低于125人的天数为![]() ,求概率
,求概率![]() ;
;
(3)现从上图的共20天的数据中任取2天的数据(甲、乙两景点中各取1天),记其中游客数不低于115且不高于135人的天数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,从参加环保知识竞赛的学生中抽出![]() 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:

(1)![]() 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛成绩的平均数、众数、中位数。(不要求写过程)
(3) 从成绩是80分以上(包括80分)的学生中选两人,求他们在同一分数段的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com