
【题目】众所周知,城市公交车的数量太多会造成资源的浪费,太少又难以满足乘客的需求,为此,某市公交公司在某站台的50名候车乘客中随机抽取10名,统计了他们的候车时间(单位:分钟),得到下表.
候车时间 | 人数 |
| 1 |
| 4 |
| 2 |
| 2 |
| 1 |
(1)估计这10名乘客的平均候车时间(同一组中的每个数据可用该组区间的中点值代替);
(2)估计这50名乘客的候车时间少于10分钟的人数.
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】[选修4—5:参数方程选讲]
在直角坐标系xoy中,曲线![]() 的参数方程是
的参数方程是 (t是参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线
(t是参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]()
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若两曲线交点为A、B,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)若函数![]() 在区间
在区间![]() 上是单调函数,试求实数
上是单调函数,试求实数![]() 的取值范围;
的取值范围;
(2)已知函数![]() ,且
,且![]() ,若函数
,若函数![]() 在区间
在区间![]() 上恰有3个零点,求实数
上恰有3个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】郑汴一体化是依托郑州省会城市资源优势发展开封的省级战略,实施至今,取得了一系列的成就:两城电信同价,金融同城,郑开大道全线贯通,城际列车实常态化运营.随着郑汴一体化的深入推进,很多人认为郑州开封未来有望合并.为了解市民对郑汴合并的态度,现随机抽查55人,结果按年龄分类统计形成如下表格:
支持 | 反对 | 合计 | |
不足35岁 | 20 | ||
35岁以上 | 30 | ||
合计 | 25 | 55 |
(1)请完成上面的2×2列联表,并判断是否有99.5%的把握认为市民对郑汴合并的态度与年龄有关?
(2)在上述样木中用分层抽样的方法,从攴持郑汴合并的两组市民中随机抽取6人作进一步调查,从这6人中任选2人,求恰有1位“不足35岁”的市民和1位“35岁及以上”的市民的概率.
附:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.814 | 5.024 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】浦东一模之后的“大将” 洗心革面,再也没进过网吧,开始发奋学习. 2019年春节档非常热门的电影《流浪地球》引发了他的思考:假定地球(设为质点![]() ,地球半径忽略不计)借助原子发动机开始流浪的轨道是以木星(看作球体,其半径约为
,地球半径忽略不计)借助原子发动机开始流浪的轨道是以木星(看作球体,其半径约为![]() 万米)的中心
万米)的中心![]() 为右焦点的椭圆
为右焦点的椭圆![]() . 已知地球的近木星点
. 已知地球的近木星点![]() (轨道上离木星表面最近的点)到木星表面的距离为
(轨道上离木星表面最近的点)到木星表面的距离为![]() 万米,远木星点
万米,远木星点![]() (轨道上离木星表面最远的点)到木星表面的距离为
(轨道上离木星表面最远的点)到木星表面的距离为![]() 万米.
万米.

(1)求如图给定的坐标系下椭圆![]() 的标准方程;
的标准方程;
(2)若地球在流浪的过程中,由![]() 第一次逆时针流浪到与轨道中心
第一次逆时针流浪到与轨道中心![]() 的距离为
的距离为![]() 万米时(其中
万米时(其中![]() 分别为椭圆的长半轴、短半轴的长),由于木星引力,部分原子发动机突然失去了动力,此时地球向着木星方向开始变轨(如图所示),假定地球变轨后的轨道为一条直线
分别为椭圆的长半轴、短半轴的长),由于木星引力,部分原子发动机突然失去了动力,此时地球向着木星方向开始变轨(如图所示),假定地球变轨后的轨道为一条直线![]() ,称该直线的斜率
,称该直线的斜率![]() 为“变轨系数”. 求“变轨系数”
为“变轨系数”. 求“变轨系数”![]() 的取值范围,使地球与木星不会发生碰撞. (精确到小数点后一位)
的取值范围,使地球与木星不会发生碰撞. (精确到小数点后一位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的最小值是
的最小值是![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)已知动直线![]() 与圆
与圆![]() :
:![]() 相切,且与椭圆
相切,且与椭圆![]() 交于
交于![]() ,
,![]() 两点.是否存在实数
两点.是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,椭圆![]() 离心率为
离心率为![]() ,
,![]() 、
、![]() 是椭圆C的短轴端点,且
是椭圆C的短轴端点,且![]() 到焦点的距离为
到焦点的距离为![]() ,点M在椭圆C上运动,且点M不与
,点M在椭圆C上运动,且点M不与![]() 、
、![]() 重合,点N满足
重合,点N满足![]() .
.
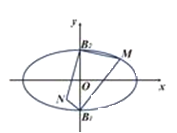
(1)求椭圆C的方程;
(2)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 有两个不同交点,求
有两个不同交点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com