
【题目】已知![]() ,
,![]() ,且f(x)=
,且f(x)=![]()
![]() .
.
(1)求函数f(x)的解析式;最小正周期及单调递增区间.
(2)当![]() 时,f(x)的最小值是-4,求此时函数f(x)的最大值,并求出相应的x的值.
时,f(x)的最小值是-4,求此时函数f(x)的最大值,并求出相应的x的值.
【答案】(1)![]() ;
;![]() ;
;![]() ;(2)
;(2)![]() ;
; ![]() .
.
【解析】
(1)利用向量数量积的定义,求出函数的 解析式,结合函数的周期公式以及单调性进行求解.
(2)求出角2x的范围,结合函数的最小值求出![]() ,结合范围求出最大值即可.
,结合范围求出最大值即可.
(1)f(x)=![]()
![]() =
=![]() sinxcosx+(m+1)(-m+1)=
sinxcosx+(m+1)(-m+1)=![]() sin2x+1-m2,
sin2x+1-m2,
最小正周期为T=![]() =π,由2kπ-
=π,由2kπ-![]() ≤2x≤2kπ+
≤2x≤2kπ+![]() ,k∈Z,
,k∈Z,
得kπ-![]() ≤x≤kπ+
≤x≤kπ+![]() ,k∈Z,
,k∈Z,
即函数的单调递增区间为![]() ;
;
(2)当![]() 时,2x∈[-
时,2x∈[-![]() ,
,![]() ],
],
则当2x=![]() 时,函数f(x)取得最小值,最小值为-4,
时,函数f(x)取得最小值,最小值为-4,
即![]() ×sin(-
×sin(-![]() )+1-m2=-4,
)+1-m2=-4,
即-![]() ×
×![]() +1-m2=-4,
+1-m2=-4,
得m2=![]() ,
,
则f(x)=![]() sin2x+1-m2=
sin2x+1-m2=![]() sin2x-
sin2x-![]()
当2x=![]() ,即x=
,即x=![]() 时,函数f(x)取得最大值,最大值为
时,函数f(x)取得最大值,最大值为![]() ×sin
×sin![]() -
-![]() =
=![]() -
-![]() =
=![]() ,
,
即![]() ,此时
,此时![]() .
.


科目:高中数学 来源: 题型:
【题目】已知双曲线E:![]() ﹣
﹣![]() =1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x.
=1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x.
(1)求双曲线E的离心率;
(2)如图,O为坐标原点,动直线l分别交直线l1 , l2于A,B两点(A,B分别在第一、第四象限),且△OAB的面积恒为8,试探究:是否存在总与直线l有且只有一个公共点的双曲线E?若存在,求出双曲线E的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,直线
的长轴长为4,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 的右顶点作互相垂直的两条直线
的右顶点作互相垂直的两条直线![]() 分别交椭圆
分别交椭圆![]() 于
于![]() 两点(点
两点(点![]() 不同于椭圆
不同于椭圆![]() 的右顶点),证明:直线
的右顶点),证明:直线![]() 过定点
过定点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:万元)的影响.对近六年的年宣传费
(单位:万元)的影响.对近六年的年宣传费![]() 和年销售量
和年销售量![]() 的数据作了初步统计,得到如下数据:
的数据作了初步统计,得到如下数据:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年宣传费 | 38 | 48 | 58 | 68 | 78 | 88 |
年销售量 | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() ,即
,即![]() .对上述数据作了初步处理,得到相关的值如下表:
.对上述数据作了初步处理,得到相关的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)规定当产品的年销售量![]() (吨)与年宣传费
(吨)与年宣传费![]() (万元)的比值在区间
(万元)的比值在区间![]() 内时认为该年效益良好.该公司某
内时认为该年效益良好.该公司某![]() 年投入的宣传费用(单位:万元)分别为:
年投入的宣传费用(单位:万元)分别为:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,试根据回归方程估计年销售量,从这
,试根据回归方程估计年销售量,从这![]() 年中任选
年中任选![]() 年,记其中选到效益良好年的数量为
年,记其中选到效益良好年的数量为![]() ,试求随机变量
,试求随机变量![]() 的分布列和期望.(其中
的分布列和期望.(其中![]() 为自然对数的底数,
为自然对数的底数,![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点. 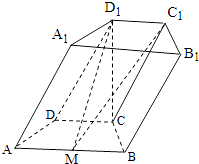
(1)求证:C1M∥平面A1ADD1;
(2)若CD1垂直于平面ABCD且CD1= ![]() ,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,求n≥m+2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国某沙漠,曾被称为“死亡之海”,截止2018年年底该地区的绿化率只有![]() ,计划从2019年开始使用无人机飞播造林,弹射的种子可以直接打入沙面里头,实现快速播种,每年原来沙漠面积的
,计划从2019年开始使用无人机飞播造林,弹射的种子可以直接打入沙面里头,实现快速播种,每年原来沙漠面积的![]() 将被改为绿洲,但同时原有绿洲面积的
将被改为绿洲,但同时原有绿洲面积的![]() 还会被沙漠化。设该地区的面积为
还会被沙漠化。设该地区的面积为![]() ,2018年年底绿洲面积为
,2018年年底绿洲面积为![]() ,经过一年绿洲面积为
,经过一年绿洲面积为![]() ……经过
……经过![]() 年绿洲面积为
年绿洲面积为![]() ,
,
(1)求经过![]() 年绿洲面积
年绿洲面积![]() ;
;
(2)截止到哪一年年底,才能使该地区绿洲面积超过![]() ?(取
?(取![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com