【题目】设F是椭圆C：
（a＞b＞0）的一个焦点，P是椭圆C上的点，圆x2＋y2＝
与线段PF交于A，B两点，若A，B三等分线段PF，则椭圆C的离心率为（ ）
A.
B.
C.
D.
【答案】D
【解析】
取线段PF的中点H，连接OH，OA，由题意可得OH⊥AB，设|OH|＝d，根据椭圆的定义以及在Rt△OHA中，可得a＝5d，在Rt△OHF中，利用勾股定理即可求解.
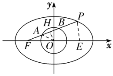
如图，取线段PF的中点H，连接OH，OA.
设椭圆另一个焦点为E，连接PE.
∵A，B三等分线段PF，∴H也是线段AB的中点，即OH⊥AB.
设|OH|＝d，则|PE|＝2d，|PF|＝2a－2d，|AH|＝
.
在Rt△OHA中，|OA|2＝|OH|2＋|AH|2，解得a＝5d.
在Rt△OHF中，|FH|＝
，|OH|＝
，|OF|＝c.
由|OF|2＝|OH|2＋|FH|2，
化简得17a2＝25c2，
.
即椭圆C的离心率为
.
故选：D.
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案科目：高中数学 来源： 题型：
【题目】下列有关命题的说法错误的是（ ）
A.若“p∨q”为假命题，则p，q均为假命题
B.“x=1”是“x≥1”的充分不必要条件
C.“sinx=
”的必要不充分条件是“x=
”
D.若命题p：x0∈R，x02≥0，则命题￢p：x∈R，x2＜0
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列五个命题：
①“
”是“
为R上的增函数”的充分不必要条件；
②函数
有两个零点；
③集合A={2，3}，B={1，2，3}，从A，B中各任意取一个数，则这两数之和等于4的概率是
；
④动圆C即与定圆
相外切，又与y轴相切，则圆心C的轨迹方程是
⑤若对任意的正数x，不等式
恒成立，则实数
的取值范围是
其中正确的命题序号是_____．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）＝a
+bx－a－ab（a≠0），当
时，f（x）>0；当
时，f（x）<0．
（1）求f（x）在
内的值域；
（2）若方程
在
有两个不等实根,求c的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
是衡量空气污染程度的一个指标，为了了解
市空气质量情况，从
年每天的值的数据中随机抽取
天的数据，其频率分布直方图如图所示.将值划分成区间
、
、
、
，分别称为一级、二级、三级和四级，统计时用频率估计概率 .
（1）根据年的数据估计该市在
年中空气质量为一级的天数；
（2）如果市对环境进行治理，经治理后，每天值
近似满足正态分布
，求经过治理后的值的均值下降率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线
的参数方程为
（
为参数），
，
为曲线上的一动点.
（I）求动点对应的参数从
变动到
时，线段
所扫过的图形面积；
（Ⅱ）若直线与曲线的另一个交点为
，是否存在点，使得为线段
的中点？若存在，求出点坐标；若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】现要完成下列三项抽样调查：①从
罐奶粉中抽取
罐进行食品安全卫生检查；②高二年级有
名学生，为调查学生的学习情况抽取一个容量为
的样本；③从某社区
户高收入家庭，
户中等收入家庭，
户低收入家庭中选出
户进行消费水平调查.以下各调查方法较为合理的是（ ）
A.①系统抽样，②简单随机抽样，③分层抽样
B.①简单随机抽样，②分层抽样，③系统抽样
C.①分层抽样，②系统抽样，③简单随机抽样
D.①简单随机抽样，②系统抽样，③分层抽样
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】进入
月份，香港大学自主招生开始报名，“五校联盟”统一对五校高三学生进行综合素质测试，在所有参加测试的学生中随机抽取了部分学生的成绩，得到如图所示的成绩频率分布直方图：
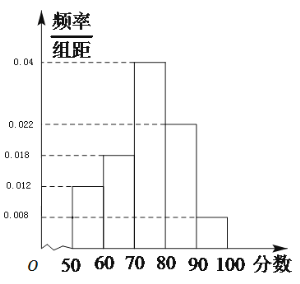
（1）估计五校学生综合素质成绩的平均值；
（2）某校决定从本校综合素质成绩排名前
名同学中，推荐
人参加自主招生考试，若已知名同学中有
名理科生，2名文科生，试求这3人中含文科生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
